Question

17．二次函數y=2$\sqrt{3}$x²的圖象如圖所示，點O為坐標原點，點A在y軸的正半軸上，點B、C在函數圖象上，四邊形OBAC為菱形，且∠OBA=120°，則點C的坐標為（-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$）．

Answer 1

分析 連結BC交OA于D，如圖，根據菱形的性質得BC⊥OA，∠OBD=60°，利用含30度的直角三角形三邊的關系得OD=$\sqrt{3}$BD，設BD=t，則OD=$\sqrt{3}$t，B（t，$\sqrt{3}$t），利用二次函數圖象上點的坐標特征得2$\sqrt{3}$t²=$\sqrt{3}$t，得出BD=$\frac{1}{2}$，OD=$\frac{\sqrt{3}}{2}$，然后根據菱形的性質得出C點坐標．

解答 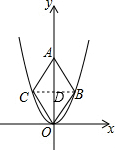解：連結BC交OA于D，如圖，
∵四邊形OBAC為菱形，
∴BC⊥OA，
∵∠OBA=120°，
∴∠OBD=60°，
∴OD=$\sqrt{3}$BD，
設BD=t，則OD=$\sqrt{3}$t，
∴B（t，$\sqrt{3}$t），
把B（t，$\sqrt{3}$t）代入y=2$\sqrt{3}$x²得2$\sqrt{3}$t²=$\sqrt{3}$t，解得t₁=0（舍去），t₂=$\frac{1}{2}$，
∴BD=$\frac{1}{2}$，OD=$\frac{\sqrt{3}}{2}$，
故C點坐標為：（-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$）．
故答案為：（-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$）．

點評 本題考查了菱形的性質、二次函數圖象上點的坐標特征，根據二次函數圖象上點的坐標性質得出BD的長是解題關鍵．