
如圖1,將三角板放在正方形ABCD上,使三角板的直角頂點E與正方形ABCD的頂點A重合,三角板的一邊交CD于點F,另一邊交CB的延長線于點G.

(1)求證:EF=EG;
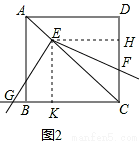
(2)如圖2,移動三角板,使頂點E始終在正方形ABCD的對角線AC上,其他條件不變.(1)中的結論是否仍然成立?若成立,情給予證明;若不成立,請說明理由;
(1)證明見解析;(2)是,證明見解析.
【解析】
試題分析:(1)由四邊形ABCD是正方形,點E與點A重合,易證得ED=EB,∠D=∠EBG=90°,又由∠GEF=90°,利用同角的余角相等,即可得∠BEG=∠DEF,然后利用ASA即可判定△BEG≌△DEF,則可證得EF=EG;
(2)首先過點E作EH⊥CD于H,作EK⊥BC于K,易證得四邊形EKCH是正方形,同(1)即可證得△GEK≌△FEH,證得EF=EG.
試題解析:(1)證明:∵四邊形ABCD是正方形,點E與點A重合,
∴ED=EB,∠D=∠EBG=90°,
∵∠GEF=90°,
∴∠BEG+∠BEF=∠BEF+∠DEF=90°,
∴∠BEG=∠DEF,
在△BEG和△DEF中,
 ,
,
∴△BEG≌△DEF(ASA),
∴EF=EG;
(2)成立.理由:
【解析】
過點E作EH⊥CD于H,作EK⊥BC于K,
∴∠EHC=∠EKC=90°,
∵四邊形ABCD是正方形,
∴∠BCD=90°,∠HCE=45°,
∴四邊形EKCH是矩形,∠HEC=∠HCE=45°,
∴EH=CH,
∴四邊形EKCH是正方形,
∴EH=EK,∠EHF=∠EKG=90°,
∵∠GEF=90°,
∴∠GEK+∠KEF=∠KEF+∠FEH=90°,
∴∠GEK=∠FEH,
在△GEK和△FEH中,
 ,
,
∴△GEK≌△FEH(ASA),
∴EF=EG.
考點:1.正方形的性質;2.全等三角形的判定與性質.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源:2014-2015學年福建省泉州市泉港區八年級上學期期中考試數學試卷(解析版) 題型:填空題
如圖,在正方形ABC1D1中,AB=1.連接AC1,以AC1為邊作第二個正方形AC1C2D2;連接AC2,以AC2為邊作第三個正方形AC2C3D3.則
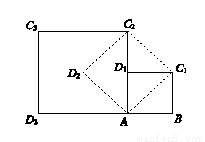
(1)第三個正方形AC2C3D3的邊長為__________;
(2)按此規律所作的第7個正方形的面積為__________.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年四川省九年級12月月考數學試卷(解析版) 題型:選擇題
二次函數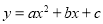 的部分對應值如下表:
的部分對應值如下表:
| … |
|
|
|
|
|
| … |
| … |
|
|
|
|
|
| … |
下面關于二次函數及其圖象說法不正確的是( )
A.對稱軸為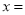 1
1
B.y的最大值是-9
C.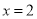 對應的函數值
對應的函數值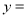 -8
-8
D.拋物線截x軸所得的線段長是6
查看答案和解析>>
科目:初中數學 來源:2014-2015學年四川省九年級上數學期末模擬數學試卷(解析版) 題型:解答題
如圖,過線段AB的兩個端點作射線AM、BN,使AM∥BN,畫∠MAB、∠NBA的平分線交于E,按下列要求回答:
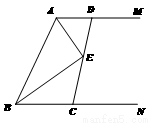
(1)∠AEB是什么角?并說明理由。
(2)過點E作一直線交AM于D,交BN于C,觀察線段DE、CE,你有何發現?
(3)無論DC的兩端點在AM、BN如何移動,只要DC經過點E,①AD+BC=AB;②AD+BC=CD誰成立?并說明理由
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省泰安市畢業生學業水平模擬二數學試卷(解析版) 題型:填空題
“上升數”是一個數中右邊數字比左邊數字大的自然數(如:34,568,2469等).任取一個兩位數,是 “上升數”的概率是
查看答案和解析>>
科目:初中數學 來源:2014-2015學年內蒙古化德縣第三中學九年級上學期期末測試數學試卷(解析版) 題型:選擇題
如圖所示,隨機閉合開關K1,K2,K3中的兩個,則能讓兩盞燈泡同時發光的概率為( )
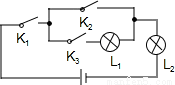
A.1 B.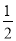 C.
C.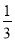 D.
D.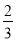
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com