
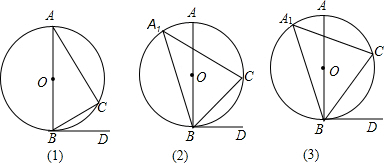
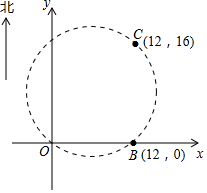 在某張航海圖上,標明了三個觀測點的坐標為O(0,0)、B(12,0)、C(12,16),由三個觀測點確定的圓形區域是“利劍-2016”中國多軍種軍事演習區,如圖所示.
在某張航海圖上,標明了三個觀測點的坐標為O(0,0)、B(12,0)、C(12,16),由三個觀測點確定的圓形區域是“利劍-2016”中國多軍種軍事演習區,如圖所示.分析 (1)根據O,B,C的坐標,即可證明△OBC是直角三角形,則OC是直徑,據此即可求解;
(2)在△OAB中,利用正弦定理即可求得AB的長;
(3)利用三角函數即可求得A點的縱坐標的值,與圓的半徑比較大小即可判斷.
解答 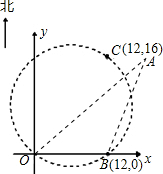 解:(1)由O(0,0),B(12,0),C(12,16)三點的坐標可知:OB⊥BC,即△OBC為直角三角形,
解:(1)由O(0,0),B(12,0),C(12,16)三點的坐標可知:OB⊥BC,即△OBC為直角三角形,
所以其外接圓的直徑 2R=OC=$\sqrt{1{2}^{2}+1{6}^{2}}$=20,
即R=10,
故所求圓形區域的面積S=πR2=100π;
(2)由圖可知,在△OAB中,∠AOB=90°-45°=45°,∠OBA=90°+30°=120°,OB=12,
則∠OAB=180°-45°-120°=15°,
根據正弦定理有$\frac{AB}{sin∠AOB}$=$\frac{OB}{sin∠OAB}$,
即$\frac{AB}{sin45°}$=$\frac{12}{sin15°}$,
解得AB=12($\sqrt{3}$+1);
(3)設A點的縱坐標為y,則
y=ABsin(180°-120°)=12($\sqrt{3}$+1)×$\frac{\sqrt{3}}{2}$=6(3+$\sqrt{3}$)>2R,
因此當可疑船由(2)中的位置向正西方向航行時,不會進入演習區.
點評 本題主要考查了解直角三角形的應用-方向角問題,正確運用正弦定理求得AB的長,是解題的關鍵.


科目:初中數學 來源: 題型:解答題
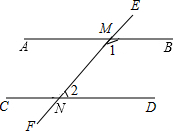 如圖,直線AB與直線EF相交于點M,直線CD與直線EF相交于點N;∠1是它的補角的2倍,∠2的余角是∠2的$\frac{1}{2}$,那么AB∥CD嗎?為什么?
如圖,直線AB與直線EF相交于點M,直線CD與直線EF相交于點N;∠1是它的補角的2倍,∠2的余角是∠2的$\frac{1}{2}$,那么AB∥CD嗎?為什么?查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 3x+6y=1 | B. | y2-3y-4=0 | C. | $\frac{1}{2}x-1=\frac{1}{x}$ | D. | 3x-2=4x+1 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
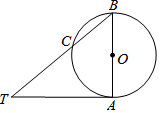 如圖,AB是⊙O的直徑,TA切⊙O與點A,連接TB交⊙O于點C,∠BTA=40°,點M是圓上異于B、C的一個動點,則∠BMC的度數等于40°或140°.
如圖,AB是⊙O的直徑,TA切⊙O與點A,連接TB交⊙O于點C,∠BTA=40°,點M是圓上異于B、C的一個動點,則∠BMC的度數等于40°或140°.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com