
【題目】如圖,CF是∠ACB的平分線,CG是∠ACB外角的平分線,FG∥BC交CG于點G,已知∠A=45°,∠B=55°,求∠FGC和∠FCG的度數. 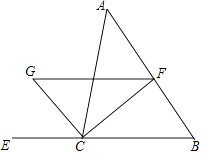
【答案】解:∵∠ACE=∠A+∠B=45°+55°=100°, 又∵CG是∠ACE的平分線,
∴∠GCE=∠ACG= ![]() ∠ACE=50°,
∠ACE=50°,
∵FG∥BC,
∴∠FGC=∠GCE=50°.
∵CF平分∠ACB,
∴∠ACF= ![]() ∠ACB,
∠ACB,
又∵∠ACG= ![]() ∠ACE,
∠ACE,
∴∠FCG=∠ACF+∠ACG= ![]() ∠ACB+
∠ACB+ ![]() ∠ACE=
∠ACE= ![]() ×180°=90°.
×180°=90°.
【解析】首先利用三角形的外角等于不相鄰的兩個內角的和求得∠ACE的度數,然后根據角的平分線的定義求得∠GCE的度數,再利用平行線的性質求得∠FGC;利用角的平分線的定義可以得到∠FCG=∠ACF+∠ACG= ![]() (∠ACB+∠ACE),從而求得∠FCG.
(∠ACB+∠ACE),從而求得∠FCG.
【考點精析】掌握平行線的性質是解答本題的根本,需要知道兩直線平行,同位角相等;兩直線平行,內錯角相等;兩直線平行,同旁內角互補.


 學業測評一課一測系列答案
學業測評一課一測系列答案 小學課時作業全通練案系列答案
小學課時作業全通練案系列答案科目:初中數學 來源: 題型:
【題目】把二次函數y=x2﹣2x+3配方成y=(x﹣m)2+k的形式,以下結果正確的是( )
A. y=﹣(x﹣1)2+4B. y=(x﹣1)2+2
C. y=(x+1)2+2D. y=(x﹣2)2+3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A.B.C分別是⊙O上的點,∠B=60°,AC=3,CD是⊙O的直徑,P是CD延長線上的一點,且AP=AC.

(1)求證:AP是⊙O的切線;
(2)求PD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,正方形ABOC的頂點A在第二象限,頂點B在x軸上,頂點C在y軸上,若正方形ABOC的面積等于7,則點A的坐標是 . 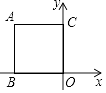
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】爸爸為了檢查小明對平行線的條件與性質這部分知識的掌握情況,給他出了一道題:如圖,AB∥DE,∠B=80°,CM平分∠BCD,CN⊥CM,求∠NCE的度數.小明稍加思索,就做出來了,你知道他是怎樣解的嗎?請把你的推理過程寫下來吧. 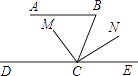
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com