
 如圖,是將菱形ABCD以點O為中心按順時針方向分別旋轉90°,180°,270°后形成的圖形.若∠BAD=60°,AB=$\sqrt{3}$,則圖中陰影部分的面積為9-3$\sqrt{3}$.
如圖,是將菱形ABCD以點O為中心按順時針方向分別旋轉90°,180°,270°后形成的圖形.若∠BAD=60°,AB=$\sqrt{3}$,則圖中陰影部分的面積為9-3$\sqrt{3}$. 分析 圖中陰影部分由4個全等的等腰三角形和一個正方形組成,如圖,作DH⊥AE于H,根據旋轉的性質得∠DAF=90°,∠EAF=∠BAD=60°,AB=AE=$\sqrt{3}$,則∠DAE=30°,在Rt△ADH中,利用含30度的直角三角形三邊的關系可得DH=$\frac{1}{2}$AD=$\frac{\sqrt{3}}{2}$,AH=$\sqrt{3}$DH=$\frac{3}{2}$,所以HE=AE-AH=$\sqrt{3}$-$\frac{3}{2}$,接著在Rt△DHE中,利用勾股定理得到DE2=DH2+HE2=6-3$\sqrt{3}$,所以圖中陰影部分的面積=4S△ADE+6-3$\sqrt{3}$=9-3$\sqrt{3}$.
解答 解:如圖,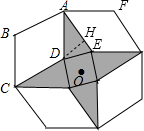 作DH⊥AE于H,
作DH⊥AE于H,
∵菱形ABCD以點O為中心按順時針方向分別旋轉90°,180°,270°,
∴∠DAF=90°,∠EAF=∠BAD=60°,AB=AE=$\sqrt{3}$
∴∠DAE=30°,
∵四邊形ABCD為菱形,
∴AD=AB=$\sqrt{3}$,
在Rt△ADH中,∵∠DAH=30°,
∴DH=$\frac{1}{2}$AD=$\frac{\sqrt{3}}{2}$,AH=$\sqrt{3}$DH=$\frac{3}{2}$,
∴HE=AE-AH=$\sqrt{3}$-$\frac{3}{2}$,
在Rt△DHE中,DE2=DH2+HE2=($\frac{\sqrt{3}}{2}$)2+($\sqrt{3}$-$\frac{3}{2}$)2=6-3$\sqrt{3}$,
∴圖中陰影部分的面積=4S△ADE+6-3$\sqrt{3}$
=4×$\frac{1}{2}$×$\sqrt{3}$×$\frac{\sqrt{3}}{2}$+6-3$\sqrt{3}$
=9-3$\sqrt{3}$.
故答案為9-3$\sqrt{3}$.
點評 本題考查了旋轉的性質:對應點到旋轉中心的距離相等;對應點與旋轉中心所連線段的夾角等于旋轉角;旋轉前、后的圖形全等.也考查了菱形的性質和含30度的直角三角形三邊的關系.


 舉一反三單元同步過關卷系列答案
舉一反三單元同步過關卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
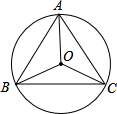 如圖是一個旋轉對稱圖形,以O為旋轉中心,以下列哪一個角為旋轉角旋轉,能使旋轉后的圖形與原圖形重合( )
如圖是一個旋轉對稱圖形,以O為旋轉中心,以下列哪一個角為旋轉角旋轉,能使旋轉后的圖形與原圖形重合( )| A. | 60° | B. | 150° | C. | 180° | D. | 240° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題

| A. | $\frac{3}{5}$ | B. | $\frac{16}{25}$ | C. | $\frac{17}{25}$ | D. | $\frac{18}{25}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com