
【題目】如圖所示,在數軸上點![]() 表示的數為-2,0,6.點
表示的數為-2,0,6.點![]() 與點
與點![]() 之間的距離表示為
之間的距離表示為![]() ,點
,點![]() 與點
與點![]() 之間的距離表示為
之間的距離表示為![]() ,點
,點![]() 與點
與點![]() 之間的距離表示為
之間的距離表示為![]() .
.
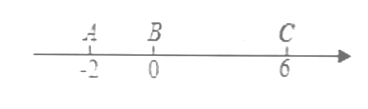
(1)請直接寫出結果,![]() .
.![]() .
.![]() .
.
(2)點![]() 為線段
為線段![]() 上的一個動點,其對應的數為
上的一個動點,其對應的數為![]() ,請化簡式子,
,請化簡式子,![]() (寫出化簡過程)
(寫出化簡過程)
(3)點![]() 開始在數軸上運動,若點
開始在數軸上運動,若點![]() 以每秒1個單位長度的速度向左運動,同時,點
以每秒1個單位長度的速度向左運動,同時,點![]() 和點
和點![]() 分別以每秒2個單位長度和5個單位長度的速度向右運動.請問:
分別以每秒2個單位長度和5個單位長度的速度向右運動.請問:![]() 的值是否隨著運動時間
的值是否隨著運動時間![]() 的變化而變化?若變化,請說明理由;若不變,請求其值
的變化而變化?若變化,請說明理由;若不變,請求其值
科目:初中數學 來源: 題型:
【題目】鴻運達酒店客房部有三人間、雙人間和單人間客房收費數據如下表:為吸引客源在“五一”黃金周進行優惠大酬賓,凡團體入住一率五折優惠。一個50人的旅游團在5月2日到該酒店住宿,租住了一些三人間、雙人間普通客房,并且每個客房剛好住滿,一天一共花去住宿費1510元。
普通間(元/人/天) | 豪華間(元/人/天) | 貴賓間(元/人/天) | |
三人間 | 50 | 100 | 500 |
雙人間 | 70 | 150 | 800 |
單人間 | 100 | 200 | 1500 |
(1)該旅游團三人間,雙人間普通客房各住了多少間?
(2)如果你作為旅游團長,你認為上面這種住宿方式是不是費用最少?
查看答案和解析>>
科目:初中數學 來源: 題型:
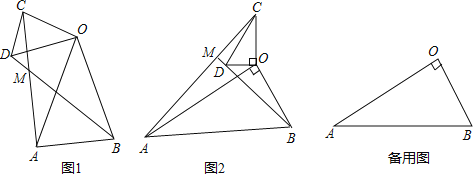
【題目】(1)問題發現
如圖1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,連接AC,BD交于點M.填空:
①![]() 的值為 ;
的值為 ;
②∠AMB的度數為 .
(2)類比探究
如圖2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,連接AC交BD的延長線于點M.請判斷![]() 的值及∠AMB的度數,并說明理由;
的值及∠AMB的度數,并說明理由;
(3)拓展延伸
在(2)的條件下,將△OCD繞點O在平面內旋轉,AC,BD所在直線交于點M,若OD=1,OB=![]() ,請直接寫出當點C與點M重合時AC的長.
,請直接寫出當點C與點M重合時AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人在筆直的湖邊公路上同起點、同終點、同方向勻速步行2400米,先到終點的人原地休息.已知甲先出發4分鐘,在整個步行過程中,甲、乙兩人的距離y(米)與甲出發的時間t(分)之間的關系如圖所示,下列結論:
①甲步行的速度為60米/分;
②乙走完全程用了32分鐘;
③乙用16分鐘追上甲;
④乙到達終點時,甲離終點還有300米
其中正確的結論有( )

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:
我們知道,四邊形的一條對角線把這個四邊形分成了兩個三角形,如果這兩個三角形相似(不全等),我們就把這條對角線叫做這個四邊形的“相似對角線”.
理解:
(1)如圖1,已知Rt△ABC在正方形網格中,請你只用無刻度的直尺在網格中找到一點D,使四邊形ABCD是以AC為“相似對角線”的四邊形(保留畫圖痕跡,找出3個即可);
(2)如圖2,在四邊形ABCD中,∠ABC=80°,∠ADC=140°,對角線BD平分∠ABC.
求證:BD是四邊形ABCD的“相似對角線”;
(3)如圖3,已知FH是四邊形EFCH的“相似對角線”,∠EFH=∠HFG=30°,連接EG,若△EFG的面積為2![]() ,求FH的長.
,求FH的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在《科學》課上,老師講到溫度計的使用方法及液體的沸點時,好奇的王紅同學準備測量食用油的沸點,已知食用油的沸點溫度高于水的沸點溫度(![]() ),王紅家只有刻度不超過
),王紅家只有刻度不超過![]() 的溫度計,她的方法是在鍋中倒入一些食用油,用煤氣灶均勻加熱,并每隔
的溫度計,她的方法是在鍋中倒入一些食用油,用煤氣灶均勻加熱,并每隔![]() 測量一次鍋中油溫,測量得到的數據如下表:
測量一次鍋中油溫,測量得到的數據如下表:
時間 | 0 | 10 | 20 | 30 | 40 |
油溫 | 10 | 30 | 50 | 70 | 90 |
王紅發現,燒了![]() 時,油沸騰了,則下列說法不正確的是( )
時,油沸騰了,則下列說法不正確的是( )
A. 沒有加熱時,油的溫度是![]()
B. 加熱![]() ,油的溫度是
,油的溫度是![]()
C. 估計這種食用油的沸點溫度約是![]()
D. 每加熱![]() ,油的溫度升高
,油的溫度升高![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
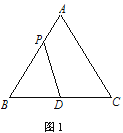
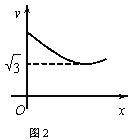
【題目】如圖1,在等邊△ABC中,D是BC的中點,P為AB 邊上的一個動點,設AP=x,圖1中線段DP的長為y,若表示y與x的函數關系的圖象如圖2所示,則△ABC的面積為( )
A. 4 B. ![]() C. 12 D.
C. 12 D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com