
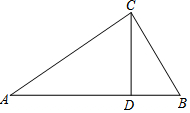
 已知:如圖,在△ABC中,CD⊥AB,∠B=2∠A.求證:AD=BD+BC.
已知:如圖,在△ABC中,CD⊥AB,∠B=2∠A.求證:AD=BD+BC. 分析 在AD上取DE=BD,然后根據線段垂直平分線上的點到線段兩端點的距離相等的性質可得BC=CE,根據等邊對等角的性質可得∠B=∠CED,然后根據三角形的一個外角等于與它不相鄰的兩個內角的和列式求出∠A=∠ACE,再根據等角對等邊的性質求出AE=CE,然后即可得證.
解答 證明:如圖,在AD上取DE=BD,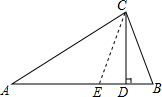
∵AD⊥AB,
∴CE=BC,
∴∠B=∠CED,
在△ACE中,∠CED=∠A+∠ACE,
又∵∠B=2∠A,
∴2∠A=∠A+∠ACE,
∴∠A=∠ACE,
∴AE=CE,
∴AD=AE+ED=CE+ED=BD+BC.
點評 本題主要考查等腰三角形的性質和判定,與線段的和差有關的問題,一般是把幾條線段轉化在一條直線來解決.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
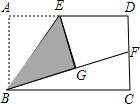 (1)操作發現:如圖,小明在矩形紙片ABCD的邊AD上取中點E,將△ABE沿BE折疊后得到△GBE,且點G在矩形ABCD內部,將BG延長交DC于點F,認為GF=DF,你同意嗎?說明理由.
(1)操作發現:如圖,小明在矩形紙片ABCD的邊AD上取中點E,將△ABE沿BE折疊后得到△GBE,且點G在矩形ABCD內部,將BG延長交DC于點F,認為GF=DF,你同意嗎?說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com