
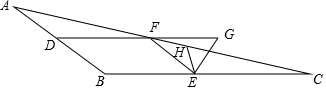
 如圖,已知:點D、E、F是△ABC的邊AB、BC、AC上的點,DF∥BC,EF∥AB,EG平分∠FEC交DF的延長線于點G,EH平分∠BEG交AC于點H,∠EHC=40°,且∠DFE-∠C=130°,則∠B的度數為144°.
如圖,已知:點D、E、F是△ABC的邊AB、BC、AC上的點,DF∥BC,EF∥AB,EG平分∠FEC交DF的延長線于點G,EH平分∠BEG交AC于點H,∠EHC=40°,且∠DFE-∠C=130°,則∠B的度數為144°. 分析 先判定四邊形BDFE是平行四邊形,得出∠B=∠DFE,再設∠B=∠DFE=α,則∠FEC=α,根據△HEF中,∠HEC+∠EHC+∠C=180°,得到$\frac{1}{2}$(180°-α)+$\frac{1}{2}$α+40°+∠C=180°,再根據∠DFE-∠C=130°,得到α-∠C=130°,最后通過解方程組,可得α=144°.
解答 解:∵DF∥BC,EF∥AB,
∴四邊形BDFE是平行四邊形,
∴∠B=∠DFE,
設∠B=∠DFE=α,則∠FEC=α,
∵EG平分∠FEC,
∴∠GEC=$\frac{1}{2}$α,∠BEG=180°-α,
∵EH平分∠BEG,
∴∠HEG=$\frac{1}{2}$(180°-α),
∵△HEF中,∠HEC+∠EHC+∠C=180°,
∴$\frac{1}{2}$(180°-α)+$\frac{1}{2}$α+40°+∠C=180°,①
又∵∠DFE-∠C=130°,
∴α-∠C=130°,②
由①+②,可得α=144°,
∴∠B的度數為144°.
故答案為:144°.
點評 本題主要考查了平行四邊形的性質,三角形內角和定理以及角平分線的定義的綜合應用,解決問題的關鍵是根據角的和差關系,列出方程組進行求解.解題時注意方程思想的靈活運用.


科目:初中數學 來源: 題型:填空題
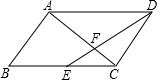 已知平行四邊形ABCD中,點E是邊BC的中點,DE與AC相交于點F,設$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{FD}$=$\frac{1}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$ (用$\overrightarrow{a}$,$\overrightarrow{b}$的式子表示)
已知平行四邊形ABCD中,點E是邊BC的中點,DE與AC相交于點F,設$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{FD}$=$\frac{1}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$ (用$\overrightarrow{a}$,$\overrightarrow{b}$的式子表示)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 計算:
計算:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系中,已知△ABC的三個頂點的坐標分別為A(-3,5),B(-2,1),C(-1,3).
如圖,在平面直角坐標系中,已知△ABC的三個頂點的坐標分別為A(-3,5),B(-2,1),C(-1,3).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,拋物線y=ax2+bx+c(a≠0)的頂點坐標為(2,-1),圖象與y軸交于點C(0,3),與x軸交于A、B兩點.
如圖,拋物線y=ax2+bx+c(a≠0)的頂點坐標為(2,-1),圖象與y軸交于點C(0,3),與x軸交于A、B兩點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com