
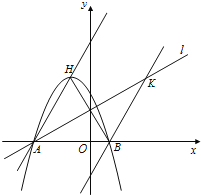
【題目】如圖,拋物線y=mx![]() +2mx-3m(m≠0)的頂點為H,與
+2mx-3m(m≠0)的頂點為H,與![]() 軸交于A、B兩點(B點在A點右側),點H、B關于直線l:
軸交于A、B兩點(B點在A點右側),點H、B關于直線l:![]() 對稱,過點B作直線BK∥AH交直線l于K點.
對稱,過點B作直線BK∥AH交直線l于K點.
(1)求A、B兩點坐標,并證明點A在直線I上。
(2)求此拋物線的解析式;
(3)將此拋物線向上平移,當拋物線經過K點時,設頂點為N,求出NK的長.
【答案】(1) A(-3,0) B(1,0) ; (2)y=-![]() x
x![]() -
-![]() x+
x+![]() ; (3)NK=4
; (3)NK=4![]()
【解析】
(1)令y=0,解關于x的一元二次方程,即可得到點A、B的坐標;然后把點A的坐標代入直線l的解析式,計算即可證明點A在直線上;
(2)根據軸對稱的性質可得AH=AB,根據直線l的解析式求出直線l與x軸的夾角為30°,然后得到∠HAB的度數是60°,過點H作HC⊥x軸于點C,然后解直角三角形求出AC、HC,從而得到OC的長度,然后寫出點H的坐標,再把點H的坐標代入拋物線解析式計算求出m的值,即可得解;
(3)根據平行直線的解析式的k值相等求出直線BK的解析式的k值,然后利用待定系數法求出直線BK的解析式,與直線l的解析式聯立求解得到點K的值,再利用拋物線解析式求出相應橫坐標上的點,從而求出拋物線向上移動的距離,然后得到平移后的拋物線的頂點N的坐標,根據兩點間的距離公式計算即可得到NK的值.
令y=0,則mx2+2mx-3m=0(m≠0),
解得x1=-3,x2=1,
∵B點在A點右側,
∴A點坐標為(-3,0),B點坐標為(1,0),
證明:∵直線l:![]()
當x=-3時,![]()
∴點A在直線l上;
(2)∵點H、B關于過A點的直線l:![]() 對稱,
對稱,
∴AH=AB=4,
設直線l與x軸的夾角為α,則![]()
所以,∠α=30°,
∴∠HAB=60°,
過頂點H作HC⊥AB交AB于C點,
則![]()
∴頂點H![]()
代入拋物線解析式,得![]()
解得m=-![]()
所以,拋物線解析式為![]()
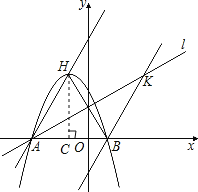
(3)∵BK∥AH
∴直線BK的k=tan60°=![]()
設直線BK的解析式為y=![]() x+b,
x+b,
∵B點坐標為(1,0),
∴![]() +b=0,
+b=0,
解得b=-![]() ,
,
∴直線BK的解析式為y=![]() x-
x-![]()
聯立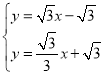
解得
∴點K的坐標為(3,2![]() ),
),
當x=3時,![]()
∴平移后與點K重合的點的坐標為(3,-6![]() ),
),
平移距離為2![]() -(-6
-(-6![]() )=8
)=8![]() ,
,
∵平移前頂點坐標為(-1,2![]() ),
),
2![]() +8
+8![]() =10
=10![]() ,
,
∴平移后頂點坐標N(-1,10![]() ),
),
![]()
所以,NK的長是4![]()


 時刻準備著暑假作業原子能出版社系列答案
時刻準備著暑假作業原子能出版社系列答案 暑假銜接教材期末暑假預習武漢出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案 假期作業暑假成長樂園新疆青少年出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案科目:初中數學 來源: 題型:
【題目】將矩形![]() 如圖放置在平面直角坐標系中,
如圖放置在平面直角坐標系中,![]() 為邊
為邊![]() 上的一個動點,過點
上的一個動點,過點![]() 作
作![]() 交
交![]() 邊于點
邊于點![]() ,且
,且![]() ,
,![]() 的長是方程
的長是方程![]() 的兩個實數根,且
的兩個實數根,且![]() .
.
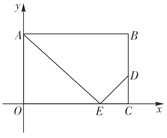
(1)設![]() ,
,![]() ,求
,求![]() 與
與![]() 的函數關系(不求
的函數關系(不求![]() 的取值范圍);
的取值范圍);
(2)當![]() 為
為![]() 的中點時,求直線
的中點時,求直線![]() 的解析式;
的解析式;
(3)在(2)的條件下,平面內是否存在點![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形為平行四邊形?若存在,請直接寫出點
為頂點的四邊形為平行四邊形?若存在,請直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解不等式組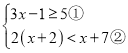
請結合題意,完成本題的解答:
(Ⅰ)解不等式①,得______;
(Ⅱ)解不等式②,得______;
(Ⅲ)把不等式①和②的解集在數軸上表示出來:
![]()
(Ⅳ)原不等式組的解集為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】著名數學教育家波利亞曾說:“對一個數學問題,改變它的形式,變換它的結構,直到發現有價值的東西,這是數學解題的一個重要原則.”
閱讀下列兩則材料,回答問題
材料一:平方運算和開方運算是互逆運算,如:a2±2ab+b2=(a±b)2,那么![]() =|a±b|,那么如何將雙重二次根式
=|a±b|,那么如何將雙重二次根式![]() (a>0,b>0,a±2
(a>0,b>0,a±2![]() >0)化簡呢?如能找到兩個數m,n(m>0,n>0),使得(
>0)化簡呢?如能找到兩個數m,n(m>0,n>0),使得(![]() 2+(
2+(![]() )2=a即m+n=a,且使
)2=a即m+n=a,且使![]() 即mn=b,那么a±2
即mn=b,那么a±2![]() =(
=(![]() )2+(
)2+(![]() )2±2
)2±2![]() =(
=(![]() 2
2
∴![]() =
=![]() =
=![]() |,雙重二次根式得以化簡.
|,雙重二次根式得以化簡.
例如化簡:![]() .∵3=1+2且2=1×2,∴3+2
.∵3=1+2且2=1×2,∴3+2![]() =(
=(![]() )2+(
)2+(![]() )2+2
)2+2![]() ,
,
∴![]() =
=![]() =1+
=1+![]() .
.
材料二:在直角坐標系xoy中,對于點P(x,y)和Q(x,y′)出如下定義:若y′=![]() ,則稱點Q為點P的“橫負縱變點”例如,點(3,2)的“橫負縱變點”為(3,2),點(﹣2,5)的“橫負縱變點”為(﹣2,﹣5)
,則稱點Q為點P的“橫負縱變點”例如,點(3,2)的“橫負縱變點”為(3,2),點(﹣2,5)的“橫負縱變點”為(﹣2,﹣5)
問題:
(1)請直接寫出點(﹣3![]() ,﹣2)的“橫負縱變點”為 ;化簡
,﹣2)的“橫負縱變點”為 ;化簡![]() = ;
= ;
(2)點M為一次函數y=﹣x+1圖象上的點,M′為點M的橫負縱變點,已知N(1,1),若M′N=![]() ,求點M的坐標;
,求點M的坐標;
(3)已知b為常數且1≤b≤2,點P在函數y=﹣x2+16(![]() +)(
+)(![]() ﹣7≤x≤a)的圖象上,其“橫負縱變點”的縱坐標y′的取值范圍是﹣32<y′≤32,若a為偶數,求a的值.
﹣7≤x≤a)的圖象上,其“橫負縱變點”的縱坐標y′的取值范圍是﹣32<y′≤32,若a為偶數,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
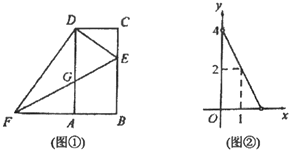
【題目】如圖①,四邊形![]() 是矩形,
是矩形,![]() ,點
,點![]() 是線段
是線段![]() 上一動點 (不與
上一動點 (不與![]() 重合),點
重合),點![]() 是線段
是線段![]() 延長線上一動點,連接
延長線上一動點,連接![]() 交
交![]() 于點
于點![]() .設
.設![]() ,已知
,已知![]() 與
與![]() 之間的函數關系如圖②所示.
之間的函數關系如圖②所示.
(1)求圖②中![]() 與
與![]() 的函數表達式;
的函數表達式;
(2)求證:![]() ;
;
(3)是否存在![]() 的值,使得
的值,使得![]() 是等腰三角形?如果存在,求出
是等腰三角形?如果存在,求出![]() 的值;如果不存在,說明理由.
的值;如果不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2﹣2ax﹣2的圖象(記為拋物線C1)頂點為M,直線l:y=2x﹣a與x軸,y軸分別交于A,B.
(1)對于拋物線C1,以下結論正確的是 ;
①對稱軸是:直線x=1;②頂點坐標(1,﹣a﹣2);③拋物線一定經過兩個定點.
(2)當a>0時,設△ABM的面積為S,求S與a的函數關系;
(3)將二次函數y=ax2﹣2ax﹣2的圖象C1繞點P(t,﹣2)旋轉180°得到二次函數的圖象(記為拋物線C2),頂點為N.
①當﹣2≤x≤1時,旋轉前后的兩個二次函數y的值都會隨x的增大而減小,求t的取值范圍;
②當a=1時,點Q是拋物線C1上的一點,點Q在拋物線C2上的對應點為Q',試探究四邊形QMQ'N能否為正方形?若能,求出t的值,若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】不覽夜景,未到重慶山城夜景,早在清乾隆時期就已有名氣,被時任巴縣知縣王爾鑒,列為巴渝十二景之一在朝天門碼頭坐船游兩江(即長江、嘉陵江),是游重慶賞夜景的一個經典項目.一艘輪船從朝天門碼頭出發勻速行駛,![]() 小時后一快艇也從朝天門碼頭出發沿同一線路勻速行駛,當快艇先到達目的地后立刻按原速返回并在途中與輪船第二次相遇.設輪船行駛的時間為
小時后一快艇也從朝天門碼頭出發沿同一線路勻速行駛,當快艇先到達目的地后立刻按原速返回并在途中與輪船第二次相遇.設輪船行駛的時間為![]()
![]() ,快艇和輪船之間的距離為
,快艇和輪船之間的距離為![]() ,
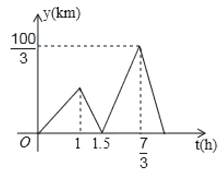
,![]() 與
與![]() 的函數關系式如圖所示,則快艇與輪船第二次相遇時到朝天門碼頭的距離為_____千米.
的函數關系式如圖所示,則快艇與輪船第二次相遇時到朝天門碼頭的距離為_____千米.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某校綜合實踐活動小組的同學欲測量公園內一棵樹DE的高度,他們在這棵樹的正前方一座樓亭前的臺階上A點處測得樹頂端D的仰角為30°,朝著這棵樹的方向走到臺階下的點C處,測得樹頂端D的仰角為60°.已知A點的高度AB為3米,臺階AC的坡度為1:![]() (即AB:BC=1:
(即AB:BC=1:![]() ),且B、C、E三點在同一條直線上.請根據以上條件求出樹DE的高度.
),且B、C、E三點在同一條直線上.請根據以上條件求出樹DE的高度.

查看答案和解析>>
科目:初中數學 來源: 題型:
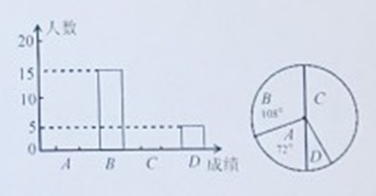
【題目】某校九年級體自模擬測試后,隨機抽取了九年級部分學生體有測試成績進行統計,得到相關的統計圖表如下:
成績/分 |
|
|
|
|
成績等級 |
|
|
|
|
請根據以上信息解答下列問題:
(1)這次統計共抽取了 名學生的體育測試成績,補全頻數分布直方圖
(2)扇形![]() 的圓心角的度數是
的圓心角的度數是
(3)若該校九年級有![]() 名學生,請據此估計該校九年級此次體育測試成績在
名學生,請據此估計該校九年級此次體育測試成績在![]() 等級以上(含
等級以上(含![]() 等級)的學生有多少人?
等級)的學生有多少人?
(4)根據測試中存在的問題,通過一段時間的針對性調練,若![]() 等級學生數可提高
等級學生數可提高![]() 等級學生數可提高
等級學生數可提高![]() ,請估計經過訓練后九年級體育測試成績在
,請估計經過訓練后九年級體育測試成績在![]() 等級以上(含
等級以上(含![]() 等級)的學生可達多少人?
等級)的學生可達多少人?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com