
 某航空公司托運行李的費用y元與托運行李的質量x(kg)之間的函數關系如圖所示,根據圖中的信息可知:免費托運行李質量應不超過19kg.
某航空公司托運行李的費用y元與托運行李的質量x(kg)之間的函數關系如圖所示,根據圖中的信息可知:免費托運行李質量應不超過19kg. 分析 由函數圖象由待定系數法可以直接求出函數的解析式;由題意得知免費托運,就是運費為0,當y=0代入求出函數的解析式就可以得出結論;
解答 解:設y與x之間的函數關系式為y=kx+b,由函數圖象,得
$\left\{\begin{array}{l}{330=30k+b}\\{630=40k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=30}\\{b=-570}\end{array}\right.$,
∴y=30x-570(x>19),
由題意,得
當y=0時,x=19,
∴免費托運行李質量的范圍是不超過19千克.
故答案為:19.
點評 本題考查了待定系數法求一次函數的解析式的運用,在解答本題時求出一次函數的解析式是關鍵.


科目:初中數學 來源: 題型:解答題
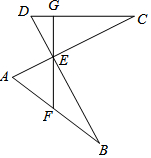 如圖,AC,BD交于點E,AC⊥BD,BE=EC,∠B=∠C,過E作EG⊥DC,垂足為G,交AB于F點.
如圖,AC,BD交于點E,AC⊥BD,BE=EC,∠B=∠C,過E作EG⊥DC,垂足為G,交AB于F點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 5.86% | B. | 5.88% | C. | 5.84% | D. | 5.82% |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
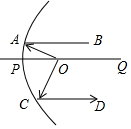 衛星信號接收鍋、汽車燈等很多燈具都與拋物線有關,如圖,從點O照射到拋物線上的光線OA、OC等反射以后沿著與POQ平行的方向射出,已知∠OAB=25°,OA⊥OC,那么∠OCD的度數是( )
衛星信號接收鍋、汽車燈等很多燈具都與拋物線有關,如圖,從點O照射到拋物線上的光線OA、OC等反射以后沿著與POQ平行的方向射出,已知∠OAB=25°,OA⊥OC,那么∠OCD的度數是( )| A. | 65° | B. | 75° | C. | 115° | D. | 135° |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
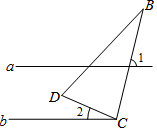 如圖所示,已知直線a,b,其中a∥b,點C在直線b上,∠DCB=90°,若∠1=75°,則∠2=( )
如圖所示,已知直線a,b,其中a∥b,點C在直線b上,∠DCB=90°,若∠1=75°,則∠2=( )| A. | 25° | B. | 15° | C. | 20° | D. | 30° |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com