
 如圖,二次函數y=(x-h)2+k的頂點坐標為M(1,-4).
如圖,二次函數y=(x-h)2+k的頂點坐標為M(1,-4).分析 (1)由條件可先求得二次函數的解析式,再令y=0可求得A、B兩點的坐標;
(2)求出△MAB的面積,再求出點P的縱坐標,然后代入拋物線解析式求解即可.
解答 解:(1)∵二次函數y=(x-h)2+k的頂點坐標為M(1,-4),
∴拋物線的表達式為y=(x-1)2-4,
令y=0,得x=-1或x=3,
∴拋物線與x軸的交點坐標為A(-1,0),B(3,0);
(2)∵A(-1,0),B(3,0),M(1,-4),
∴AB=4.
∴S△MAB=8,
∵AB=4,
∴點P到AB的距離為5時,S△PAB=$\frac{5}{4}{S_{△MAB}}$,
即點P的縱坐標為±5.
∵點P在二次函數的圖象上,且頂點坐標為M(1,-4),
∴點P的縱坐標為5,
∴5=(x-1)2-4,
∴x1=-2,x2=4.
∴點P的坐標為(4,5)或(-2,5).
點評 本題主要考查待定系數法求函數解析式及二次函數圖象上點的坐標,掌握二次函數頂點式y=a(x-h)2+k的頂點坐標為(h,k)是解題的關鍵.


 浙大優學小學年級銜接捷徑浙江大學出版社系列答案
浙大優學小學年級銜接捷徑浙江大學出版社系列答案科目:初中數學 來源: 題型:解答題
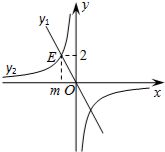 如圖,正比例函數y1=-2x與反比例函數y2相交于點E(m,2).
如圖,正比例函數y1=-2x與反比例函數y2相交于點E(m,2).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 拋物線與x軸有兩個交點 | B. | 當x=1時,函數有最大值 | ||
| C. | 拋物線可由$y=-\frac{1}{2}{x^2}$經過平移得到 | D. | 當-1<x≤2時,函數y的整數值有3個 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
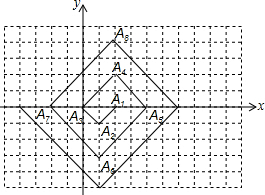 如圖,在一單位長度為1的方格紙上.△A1A2A3,△A3A4A5,△A5A6A7…都是斜邊在x軸上,斜邊長分別為2,4,6…的等腰直角三角形.若△A1A2A3的頂點坐標分別為A1(2,0),A2(1,-1),A3(0,0).則依圖中所示規律,A2016的坐標是(2,1008).
如圖,在一單位長度為1的方格紙上.△A1A2A3,△A3A4A5,△A5A6A7…都是斜邊在x軸上,斜邊長分別為2,4,6…的等腰直角三角形.若△A1A2A3的頂點坐標分別為A1(2,0),A2(1,-1),A3(0,0).則依圖中所示規律,A2016的坐標是(2,1008).查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,正方形ABCD的頂點A,B與正方形EFGH的頂點G,H同在一段拋物線上,且拋物線的頂點同時落在CD和y軸上,正方形邊AB與EF同時落在x軸上,若正方形ABCD的邊長為4,則正方形EFGH的邊長為2$\sqrt{5}$-2.
如圖,正方形ABCD的頂點A,B與正方形EFGH的頂點G,H同在一段拋物線上,且拋物線的頂點同時落在CD和y軸上,正方形邊AB與EF同時落在x軸上,若正方形ABCD的邊長為4,則正方形EFGH的邊長為2$\sqrt{5}$-2.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
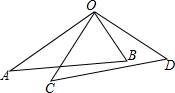 如圖所示,將一副三角板疊放在一起,使直角頂點重合,且∠AOD=2∠BOC,則∠AOC的等于( )
如圖所示,將一副三角板疊放在一起,使直角頂點重合,且∠AOD=2∠BOC,則∠AOC的等于( )| A. | 45° | B. | 30° | C. | 25° | D. | 20° |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com