
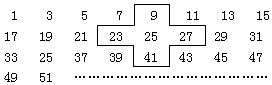
分析 (1)根據(jù)中間數(shù)a左右相鄰的兩個數(shù)相差2,上下相鄰的兩個數(shù)相差16,進而填空;
(2)根據(jù)和為3000、425列出方程求得a的值,根據(jù)數(shù)列為奇數(shù)且第n行的第一個數(shù)為16n-15和最后一個數(shù)為16n-1檢驗是否符合題意.
(3)與(2)同理可得.
解答 解:(1)根據(jù)圖中數(shù)據(jù)可知,中間數(shù)a左右相鄰的兩個數(shù)相差2,上下相鄰的兩個數(shù)相差16,
即a-16;a+16;a-2;a+2,
故答案為a-16;a+16;a-2;a+2;
(2)根據(jù)題意得:a-16+a+16+a-2+a+2=3000,即5a=3000,
解得:a=600,不是奇數(shù),
∴這5個數(shù)的和不會是3000;
若5a=425,則a=85,
∵第n行的第一個數(shù)為1+16(n-1)=16n-15,最后一個數(shù)為15+16(n-1)=16n-1,
∴當16n-15=85時,n=6.25,不是整數(shù);
當16n-1=85時,n=5.375,不是整數(shù);
∴85不是第一個又不是最后一個,
∴這5個數(shù)的和可以是425;
(3)根據(jù)題意得:5a=1844325,
解得:a=368865,
∵當16n-15=368865時,n=23055,是整數(shù),
即368865是第23055行第1個數(shù),
故這五個數(shù)的和不可能是1844325.
點評 本題考查一元一次方程的應用,關鍵是看到表格中中間位置的數(shù)和四周數(shù)的關系,最后可列出方程求解.


科目:初中數(shù)學 來源: 題型:解答題
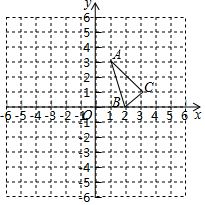 如圖,把△ABC向下平移2個單位長度,再向左平移4個單位長度得△A′B′C′,解答下列各題.
如圖,把△ABC向下平移2個單位長度,再向左平移4個單位長度得△A′B′C′,解答下列各題.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 同為負數(shù) | B. | 一個正數(shù)一個負數(shù) | ||
| C. | 同為正數(shù) | D. | 一個負數(shù)一個是零 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
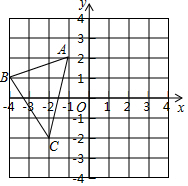 如圖,已知△ABC的三個頂點的坐標為A(-1,2),B(-4,1),C(-2,-2).
如圖,已知△ABC的三個頂點的坐標為A(-1,2),B(-4,1),C(-2,-2).查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com