精英家教網 > 初中數學 > 題目詳情

如圖，已知分別以DABC的三個頂點為圓心，6cm為半徑作三個等圓，與三邊的交點分別是E、G、N、M、F，求EF、GH、MN的弧的長度的和。

答案：
解析：

6pcm

練習冊系列答案

金榜一號同步單元全程達標測試AB卷系列答案

亮點激活3加1大試卷系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：初中數學 來源： 題型：

（2011•裕華區二模）如圖①，將兩個等腰直角三角形疊放在一起，使上面三角板的一個銳角頂點與下面三角板的直角頂點重合，并將上面的三角板繞著這個頂點逆時針旋轉，在旋轉過程中，當下面三角板的斜邊被分成三條線段時，我們來研究這三條線段之間的關系．
（1）實驗與操作：
如圖②，如果上面三角板的一條直角邊旋轉到CM的位置時，它的斜邊恰好旋轉到CN的位置，請在網格中分別畫出以AM、MN和NB為邊長的正方形，觀察這三個正方形的面積之間的關系；
（2）猜想與探究：
如圖③，在Rt△ABC中，BC=AC，∠ACB=90°，M、N是AB邊上的點，∠MCN=45°，作DA⊥AB于點A，截取DA=NB，并連接DC、DM．
我們來證明線段CD與線段CN相等．
∵∠CAB=∠CBA=45°，又DA⊥AB于點A，
∴∠DAC=45°，∴∠DAC=∠CBA，
又∵DA=NB，BC=AC，
∴△CAD≌△CBN．
∴CD=CN．

請你繼續解答：
①線段MD與線段MN相等嗎？為什么？
②線段AM、MN、NB有怎樣的數量關系，為什么？
（3）拓廣與運用：
如圖④，已知線段AB上任意一點M（AM＜MB），是否總能在線段MB上找到一點N，使得分別以AM與BN為邊長的正方形的面積的和等于以MN為邊長的正方形的面積？若能，請在圖④中畫出點N的位置，并簡要說明作法；若不能，請說明理由．

查看答案和解析>>

科目：初中數學 來源： 題型：

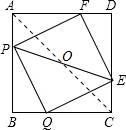如圖，已知有四個動點P、Q、E、F分別從正方形ABCD的頂點A、B、C、D同時出發，沿AB、BC、CD、DA以同樣的速度勻速向B、C、D、A移動．
（1）求證：四邊形PQEF是正方形．
（2）PE是否總過某一點，并說明理由．
（3）四邊形PQEF的頂點在何處時，其面積有最小值和最大值，并求其最小值和最大值．

查看答案和解析>>

科目：初中數學 來源： 題型：解答題

如圖①，將兩個等腰直角三角形疊放在一起，使上面三角板的一個銳角頂點與下面三角板的直角頂點重合，并將上面的三角板繞著這個頂點逆時針旋轉，在旋轉過程中，當下面三角板的斜邊被分成三條線段時，我們來研究這三條線段之間的關系．
（1）實驗與操作：
如圖②，如果上面三角板的一條直角邊旋轉到CM的位置時，它的斜邊恰好旋轉到CN的位置，請在網格中分別畫出以AM、MN和NB為邊長的正方形，觀察這三個正方形的面積之間的關系；
（2）猜想與探究：
如圖③，在Rt△ABC中，BC=AC，∠ACB=90°，M、N是AB邊上的點，∠MCN=45°，作DA⊥AB于點A，截取DA=NB，并連接DC、DM．
我們來證明線段CD與線段CN相等．
∵∠CAB=∠CBA=45°，又DA⊥AB于點A，
∴∠DAC=45°，∴∠DAC=∠CBA，
又∵DA=NB，BC=AC，
∴△CAD≌△CBN．
∴CD=CN．

請你繼續解答：
①線段MD與線段MN相等嗎？為什么？
②線段AM、MN、NB有怎樣的數量關系，為什么？
（3）拓廣與運用：
如圖④，已知線段AB上任意一點M（AM＜MB），是否總能在線段MB上找到一點N，使得分別以AM與BN為邊長的正方形的面積的和等于以MN為邊長的正方形的面積？若能，請在圖④中畫出點N的位置，并簡要說明作法；若不能，請說明理由．

查看答案和解析>>

科目：初中數學 來源： 題型：

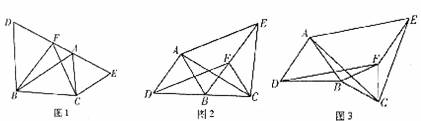
如圖1，點D、F、A、E在同一直線上，且AE=DF，分別以DA、AE為一邊，在直線DE

的同側作等邊△DBA和等邊△ACE，試證明△BCF也是等邊三角形。

（1）下面是小偉對此題的分析過程，請你根據他的分析填空：此題中，要想證明△BCF是等邊三角形，至少要證明兩條邊相等。欲證兩條邊相等，可以通過證明這兩條邊所在的兩個三角形全等來實現。根據已知條件，在不加輔助線的情況下，不妨嘗試證明 ≌△ABC，依據是（寫出定義、公理或定理的內容）；

（2）如圖2，點D、B、C在同一直線上，分別以DB、BC為一邊，在直線DC的同側作等邊△DBA和等邊△BCF，再以DA、DF為鄰邊作□ADFE，求證：△ACE是等邊三角形；

（3）如圖3是將（2）中的等邊△BCF繞點B順時針旋轉一個角度后得到的圖形，若其他條件不變，△ACE是否還是等邊三角形?請加以說明。

查看答案和解析>>

科目：初中數學 來源：2011年河北省石家莊市裕華區中考數學二模試卷（解析版） 題型：解答題

如圖①，將兩個等腰直角三角形疊放在一起，使上面三角板的一個銳角頂點與下面三角板的直角頂點重合，并將上面的三角板繞著這個頂點逆時針旋轉，在旋轉過程中，當下面三角板的斜邊被分成三條線段時，我們來研究這三條線段之間的關系．
（1）實驗與操作：
如圖②，如果上面三角板的一條直角邊旋轉到CM的位置時，它的斜邊恰好旋轉到CN的位置，請在網格中分別畫出以AM、MN和NB為邊長的正方形，觀察這三個正方形的面積之間的關系；
（2）猜想與探究：
如圖③，在Rt△ABC中，BC=AC，∠ACB=90°，M、N是AB邊上的點，∠MCN=45°，作DA⊥AB于點A，截取DA=NB，并連接DC、DM．
我們來證明線段CD與線段CN相等．
∵∠CAB=∠CBA=45°，又DA⊥AB于點A，
∴∠DAC=45°，∴∠DAC=∠CBA，
又∵DA=NB，BC=AC，
∴△CAD≌△CBN．
∴CD=CN．

查看答案和解析>>

同步練習冊答案

日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

練習冊

高中

初中

小學