
【題目】方程(組)與不等式(組)是代數的重要組成部分,也是解決數學問題的重要工具,請利用所學,解決以下 3 個問題:
(1)當 k 為何整數時,關于 x , y 的方程組![]() 的解滿足 x y 且 x y 4 ;
的解滿足 x y 且 x y 4 ;
(2)已知正整數 a ,使得關于 x , y 的方程組![]() 的解是整數,解關于 x 的不等式
的解是整數,解關于 x 的不等式![]() ;
;
(3)已知 x ,y ,z 為 3 個非負實數,且滿足3x 2 y z 5 ,x y z 2 ,記 S 2x y z對于符合題意的任意實數 S ,不等式 2m S 3 始終成立,試確定 m 的取值范圍.
【答案】(1) -6<k<-4;(2) x≥1;(3) m≤![]() .
.
【解析】
(1)將k看做已知數求出方程組的解表示出x與y,根據題意列出不等式組,求出不等式組的解集即可;
(2)將a看做已知數求出方程組的解表示出x與y,代入不等式,解不等式即可;
(3)解方程組得到x,y,z,再解不等式組,得到S,代入不等式解答即可.
解:(1)解方程組![]() 得
得![]() ,
,
∵x>y且x-y<4,
∴![]() ,
,
解答:-6<k<-4;
(2)解方程組![]() 得,
得, ,
,
∵a為正整數,x、y為整數,
∴a=2,
把a=2代入![]() ≤
≤![]() 得
得![]() ≤
≤![]() ,
,
解得:x≥1;
(3)解方程組
得, ,
,
∵x,y,z為3個非負實數,
∴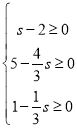 ,解得:2≤S≤3,
,解得:2≤S≤3,
∴S最小=2,S的最大值3,
∵2m-S≤3始終成立,
∴2m-3≤2,
解得:m≤![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】據調查,超速行駛是引發交通事故的主要原因之一,所以規定以下情境中的速度不得超過15m/s在一條筆直公路BD的上方A處有一探測儀,如平面幾何圖,AD=24m,∠D=90°,第一次探測到一輛轎車從B點勻速向D點行駛,測得∠ABD=31°,2秒后到達C點,測得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,結果精確到1m).
(1)求B,C的距離.
(2)通過計算,判斷此轎車是否超速.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖8,AB兩地之間有一座山,以前從A地到B地需要經過C地.現在政府出資打通了一條山嶺隧道,使從A地到B地可沿直線AB直接到達.已知BC=8km,∠A=45°,∠B=53°.
(1)求點C到直線AB的距離;
(2)求現在從A地到B地可比原來少走多少路程?(結果精確到0.1km;參考數據:![]() ≈1.41,sin53°≈0.80,cos53°≈0.60)
≈1.41,sin53°≈0.80,cos53°≈0.60)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:若有理數a,b滿足等式![]() ,則稱a,b是“雉水有理數對”,記作
,則稱a,b是“雉水有理數對”,記作![]() 如:數對
如:數對![]() ,
,![]() 都是“雉水有理數對”.
都是“雉水有理數對”.
![]() 數對
數對![]() ______
______![]() 填“是”或“不是”
填“是”或“不是”![]() “雉水有理數對”;
“雉水有理數對”;
![]() 若
若![]() 是“雉水有理數對”,求m的值;
是“雉水有理數對”,求m的值;
![]() 請寫出一個符合條件的“錐水有理數對”______
請寫出一個符合條件的“錐水有理數對”______![]() 注意:不能與題目中已有的“雉水有理數對”重復
注意:不能與題目中已有的“雉水有理數對”重復![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
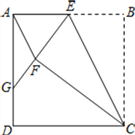
【題目】如圖,正方形ABCD中,點E為AB上一動點(不與A、B重合).將△EBC沿CE翻折至△EFC,延長EF交邊AD于點G.
(1)連結AF,若 AF∥CE.證明:點E為AB的中點;
(2)證明:GF=GD;
(3)若AD=10,設EB=x,GD=y,求y與x的函數關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(閱讀理解)對于任意正實數a、b,
∵(![]() ﹣
﹣![]() )2≥0,
)2≥0,
∴a﹣2![]() +b≥0,
+b≥0,
∴a+b≥2![]() ,(只有當a=b時,a+b等于2
,(只有當a=b時,a+b等于2![]() ).
).
(1)(獲得結論)在a+b≥2![]() (a、b均為正實數)中,若ab為定值p,
(a、b均為正實數)中,若ab為定值p,
則a+b≥2![]() ,只有當a=b時,a+b有最小值2
,只有當a=b時,a+b有最小值2![]() .
.
根據上述內容,回答下列問題:若m>0,只有當m= 時,m+![]() 有最小值 .
有最小值 .
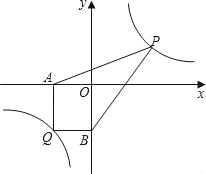
(2)(探索應用)已知點Q(﹣3,﹣4)是雙曲線y=![]() 上一點,過Q作QA⊥x軸于點A,作QB⊥y軸于點B.點P為雙曲線y=
上一點,過Q作QA⊥x軸于點A,作QB⊥y軸于點B.點P為雙曲線y=![]() (x>0)上任意一點,連接PA,PB,求四邊形AQBP的面積的最小值.
(x>0)上任意一點,連接PA,PB,求四邊形AQBP的面積的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,∠BAC的平分線交BC于點D,點O在AB上,以點O為圓心,OA為半徑的圓恰好經過點D,分別交AC,AB于點E,F.
(1)試判斷直線BC與⊙O的位置關系,并說明理由;
(2)若BD=2![]() ,BF=2,求陰影部分的面積(結果保留π).
,BF=2,求陰影部分的面積(結果保留π).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A、B在數軸上表示的數分別為﹣12和8,兩只螞蟻M、N分別從A、B兩點同時勻速出發,同向而行
時間/秒 | 0 | 1 | 5 |
A點位置 | ﹣12 | ﹣9 |
|
B點位置 | 8 |
| 18 |
(1)請填寫表格;
(2)若兩只螞蟻在數軸上點P相遇,求點P在數軸上表示的數;
![]()
(3)若運動t秒鐘時,兩只螞蟻的距離為10,求出t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 兩點在數軸上所表示的數分別為
兩點在數軸上所表示的數分別為![]() 且滿足
且滿足![]() .
.
(1)則![]() ,
,![]() ;
;
(2)若點![]() 從
從![]() 點出發,以每秒1個單位長度的速度向右運動,同時點Q從M點出發,以每秒1個單位長度的速度向左運動,經過多長時間后
點出發,以每秒1個單位長度的速度向右運動,同時點Q從M點出發,以每秒1個單位長度的速度向左運動,經過多長時間后![]() 兩點相距7個單位長度?
兩點相距7個單位長度?
(3)若![]() 為線段
為線段![]() 上的兩點,且
上的兩點,且![]() ,點
,點![]() 從點
從點![]() 出發,以每秒2個單位長度的速度向左運動,點
出發,以每秒2個單位長度的速度向左運動,點![]() 從
從![]() 點出發,以每秒4個單位長度的速度向右運動,點R從B點出發,以每秒3個單位長度的速度向右運動,P,Q,R同時出發,是否存在常數
點出發,以每秒4個單位長度的速度向右運動,點R從B點出發,以每秒3個單位長度的速度向右運動,P,Q,R同時出發,是否存在常數![]() ,使得
,使得![]()
![]() 的值與它們的運動時間無關,為定值。若存在,請求出
的值與它們的運動時間無關,為定值。若存在,請求出![]() 和這個定值;若不存在,請說明理由.
和這個定值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com