
某賓館有50個房間供游客住宿,當每個房間的房價為每天180元時,房間會全部住滿.當每個房間 每天的房價每增加10元時,就會有一個房間空閑.賓館需對游客居住的每個房間每天支出20元的各種費用.根據規定,每個房間每天的房價不得高于340元.設每個房間的房價增加x元(x為10的正整數倍).
(1)設一天訂住的房間數為y,直接寫出y與x的函數關系式及自變量x的取值范圍;
(2)設賓館一天的利潤為w元,求w與x的函數關系式;
(3)一天訂住多少個房間時,賓館的利潤最大?最大利潤是多少元?
(1)y=50-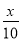 ,且0≤x≤160,且x為10的正整數倍.(2)w=-
,且0≤x≤160,且x為10的正整數倍.(2)w=-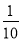 x2+34x+8000;(3)一天訂住34個房間時,賓館每天利潤最大,最大利潤為10880元.
x2+34x+8000;(3)一天訂住34個房間時,賓館每天利潤最大,最大利潤為10880元.
【解析】
試題分析:(1)理解每個房間的房價每增加x元,則減少房間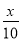 間,則可以得到y與x之間的關系;
間,則可以得到y與x之間的關系;
(2)每個房間訂住后每間的利潤是房價減去20元,每間的利潤與所訂的房間數的積就是利潤;
(3)求出二次函數的對稱軸,根據二次函數的增減性以及x的范圍即可求解.
試題解析:(1)由題意得:
y=50-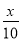 ,且0≤x≤160,且x為10的正整數倍.
,且0≤x≤160,且x為10的正整數倍.
(2)w=(180-20+x)(50-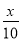 ),即w=-
),即w=-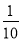 x2+34x+8000;
x2+34x+8000;
(3)w=-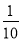 x2+34x+8000=-
x2+34x+8000=-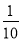 (x-170)2+10890
(x-170)2+10890
拋物線的對稱軸是:x=170,拋物線的開口向下,當x<170時,w隨x的增大而增大,
但0≤x≤160,因而當x=160時,即房價是340元時,利潤最大,
此時一天訂住的房間數是:50-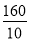 =34間,
=34間,
最大利潤是:34×(340-20)=10880元.
答:一天訂住34個房間時,賓館每天利潤最大,最大利潤為10880元.
考點:二次函數的應用.


科目:初中數學 來源:2014-2015學年江蘇省八年級12月月考數學試卷(解析版) 題型:填空題
在直角坐標系中,點A(-3,m)與點B(n,1)關于x軸對稱,則m+n =_______,
查看答案和解析>>
科目:初中數學 來源:2014-2015學年四川省仁壽縣聯誼學校九年級上學期期中考試數學試卷(解析版) 題型:解答題
如圖,在梯形ABCD中,AD//BC,AB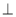 AD,對角線BD
AD,對角線BD 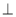 DC,
DC,

(1)試說明:ΔABD∽ΔDCB;
(2)若BD=7,AD=5,求BC的長。
查看答案和解析>>
科目:初中數學 來源:2014-2015學年四川省仁壽縣聯誼學校九年級上學期期中考試數學試卷(解析版) 題型:選擇題
關于的一元二次方程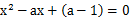 的根的情況是( )
的根的情況是( )
A.有兩個不相等的實數根
B.有兩個相等的實數根
C.沒有實數根
D.有兩個實數根
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江西省九年級上學期第二次月考數學試卷(解析版) 題型:解答題
已知拋物線拋物線y n=-(x-an)2+an(n為正整數,且0<a1<a2<…<an)與x軸的交點為An-1(bn-1,0)和An(bn,0),當n=1時,第1條拋物線y1=-(x-a1)2+a1與x軸的交點為A0(0,0)和A1(b1,0),其他依此類推.
(1)求a1,b1的值及拋物線y2的解析式;
(2)拋物線y3的頂點坐標為( , );
依此類推第n條拋物線yn的頂點坐標為( , );
所有拋物線的頂點坐標滿足的函數關系是 ;
(3)探究下列結論:
若用An-1An表示第n條拋物線被x軸截得得線段長,直接寫出A0A1的值,并求出An-1An;
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省九年級12月月考數學試卷(解析版) 題型:填空題
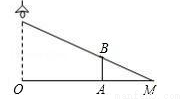
如圖,路燈距離地面8米,身高1.6米的小明站在距離燈的底部(點O)20米的A處,則小明的影子AM長為
查看答案和解析>>
科目:初中數學 來源:2013-2014學年湖北省咸寧市九年級上學期第四次月考數學試卷(解析版) 題型:解答題
(10分)在△ABC中,∠BAC=90°,,AB=AC=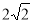 ,圓的半徑為1,如圖所示,若點O在BC邊上運動(與點B、C不重合),設OB=x,△AOC的面積為y.
,圓的半徑為1,如圖所示,若點O在BC邊上運動(與點B、C不重合),設OB=x,△AOC的面積為y.
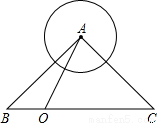
(1)求y關于x的函數解析式,并寫出自變量的取值范圍;(4分)
(2)以點O為圓心,BO長為半徑作圓,求當圓O與圓A相切時,△AOC的面積.(6分)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com