
【題目】如圖,在![]() 中,
中,![]() 為銳角,點
為銳角,點![]() 為射線
為射線![]() 上一動點,連接
上一動點,連接![]() .以
.以![]() 為直角邊且在
為直角邊且在![]() 的上方作等腰直角三角形
的上方作等腰直角三角形![]() .
.
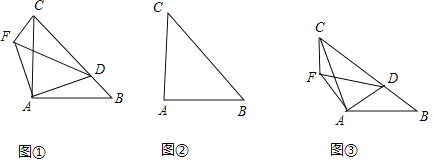
(1)若![]() ,
,![]()
①當點![]() 在線段
在線段![]() 上時(與點
上時(與點![]() 不重合),試探討
不重合),試探討![]() 與
與![]() 的數量關系和位置關系;
的數量關系和位置關系;
②當點![]() 在線段
在線段![]() 的延長線上時,①中的結論是否仍然成立,請在圖2中面出相應的圖形并說明理由;
的延長線上時,①中的結論是否仍然成立,請在圖2中面出相應的圖形并說明理由;
(2)如圖3,若![]() ,
,![]() ,
,![]() ,點
,點![]() 在線段
在線段![]() 上運動,試探究
上運動,試探究![]() 與
與![]() 的位置關系.
的位置關系.
【答案】(1)①CF⊥BD,證明見解析;②成立,理由見解析;(2)CF⊥BD,證明見解析.
【解析】
(1)①根據同角的余角相等求出∠CAF=∠BAD,然后利用“邊角邊”證明△ACF和△ABD全等,②先求出∠CAF=∠BAD,然后與①的思路相同求解即可;
(2)過點A作AE⊥AC交BC于E,可得△ACE是等腰直角三角形,根據等腰直角三角形的性質可得AC=AE,∠AED=45°,再根據同角的余角相等求出∠CAF=∠EAD,然后利用“邊角邊”證明△ACF和△AED全等,根據全等三角形對應角相等可得∠ACF=∠AED,然后求出∠BCF=90°,從而得到CF⊥BD.
解:(1)①∵∠BAC=90°,△ADF是等腰直角三角形,
∴∠CAF+∠CAD=90°,∠BAD+∠ACD=90°,
∴∠CAF=∠BAD,
在△ACF和△ABD中,
∵AB=AC,∠CAF=∠BAD,AD=AF,
∴△ACF≌△ABD(SAS),
∴CF=BD,∠ACF=∠ABD=45°,
∵∠ACB=45°,
∴∠FCB=90°,
∴CF⊥BD;
②成立,理由如下:如圖2:
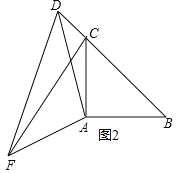
∵∠CAB=∠DAF=90°,
∴∠CAB+∠CAD=∠DAF+∠CAD,
即∠CAF=∠BAD,
在△ACF和△ABD中,
∵AB=AC,∠CAF=∠BAD,AD=AF,
∴△ACF≌△ABD(SAS),
∴CF=BD,∠ACF=∠B,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∴∠BCF=∠ACF+∠ACB=45°+45°=90°,
∴CF⊥BD;
(2)如圖3,過點A作AE⊥AC交BC于E,

∵∠BCA=45°,
∴△ACE是等腰直角三角形,
∴AC=AE,∠AED=45°,
∵∠CAF+∠CAD=90°,∠EAD+∠CAD=90°,
∴∠CAF=∠EAD,
在△ACF和△AED中,
∵AC=AE,∠CAF=∠EAD,AD=AF,
∴△ACF≌△AED(SAS),
∴∠ACF=∠AED=45°,
∴∠BCF=∠ACF+∠BCA=45°+45°=90°,
∴CF⊥BD.


科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,A(1,2),B(3,1),C(-2,-1).

(1)在圖中作出△ABC 關于 y 軸對稱的△A1B1C1并寫出坐標;
(2)求出△A1B1C1的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC在平面直角坐標系中的位置如圖所示.
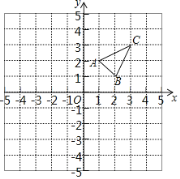
(1)作出與△ABC關于x軸對稱的△A1B1C1;
(2)將△ABC向左平移4個單位長度,畫出平移后的△A2B2C2;
(3)若在如圖的網格中存在格點P,使點P的橫、縱坐標之和等于點C的橫、縱坐標之和,請寫出所有滿足條件的格點P的坐標(C除外).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 如圖
如圖![]() ,
,![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于點
于點![]() ,在
,在![]() 上截取
上截取![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于點
于點![]() .求證:四邊形
.求證:四邊形![]() 是菱形;
是菱形;
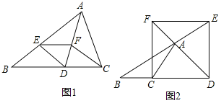
![]() 如圖
如圖![]() ,
,![]() 中,
中,![]() 平分
平分![]() 的外角
的外角![]() 交
交![]() 的延長線于點
的延長線于點![]() ,在
,在![]() 的延長線上截取
的延長線上截取![]() ,過點
,過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() .四邊形
.四邊形![]() 還是菱形嗎?如果是,請證明;如果不是,請說明理由.
還是菱形嗎?如果是,請證明;如果不是,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】湘一“追逐夢想”數學興趣小組編了一個“詩·遠方”的計算程序,規定:輸入數據![]() ,
,![]() 時,若輸出的是代數式稱為“詩
時,若輸出的是代數式稱為“詩![]() ”,若輸出的是等式稱為“遠方
”,若輸出的是等式稱為“遠方![]() ”.
”.
回答下列問題:
(1)當輸入正整數![]() ,
,![]() 時,得到“遠方
時,得到“遠方![]() ”和“詩
”和“詩![]() ”,若“遠方
”,若“遠方![]() ”為
”為![]() ,求證“詩
,求證“詩![]() ”:
”:![]() 是完全平方式.(溫馨提示:對于一個整式
是完全平方式.(溫馨提示:對于一個整式![]() ,如果存在另一個整式
,如果存在另一個整式![]() ,使
,使![]() 的條件,則稱
的條件,則稱![]() 是完全平方式,比如
是完全平方式,比如![]() ,
,![]() 是完全平方式.)
是完全平方式.)
(2)當輸入![]() ,
,![]() 時,求“遠方
時,求“遠方![]() ”:
”:![]() 的
的![]() ,
,![]() 的正整數解.
的正整數解.
(3)若正數![]() ,
,![]() 互為倒數,求“詩
互為倒數,求“詩![]() ”:
”:![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“鄂爾多斯,溫暖全世界”這句廣告語及上乘的質量使鄂爾多斯的羊絨制品聞名中外,我市某羊絨企業的工廠店在銷售中發現:某種羊絨圍巾平均每天可售出![]() 件,每件可獲利
件,每件可獲利![]() 元;若售價減少
元;若售價減少![]() 元,平均每天就可多售出
元,平均每天就可多售出![]() 件;若想平均每天銷售這種圍巾盈利
件;若想平均每天銷售這種圍巾盈利![]() 元,并使顧客得到更大的實惠,那么每件圍巾應降價多少元?若想獲利最大,應降價多少?
元,并使顧客得到更大的實惠,那么每件圍巾應降價多少元?若想獲利最大,應降價多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某電器超市銷售A B兩種型號的電風扇,A型號每臺進價為200元,B型號每臺進價分別為150元,下表是近兩天的銷售情況:
銷售時段 | 銷售數量 | 銷售收入 | |
A種型號 | B種型號 | ||
第一天 | 3臺 | 5臺 | 1620元 |
第二天 | 4臺 | 10臺 | 2760元 |
(進價、售價均保持不變,利潤=銷售收入-進貨成本)
(1)求A、B兩種型號的電風扇的銷售單價;
(2)若超市準備用不多于5400元的金額再采購這兩種型號的電風扇共30臺,求A種型號的電風扇最多能采購多少臺?
(3)在(2)的條件下,超市銷售完這30臺電風扇能否實現利潤不少于1060元的目標?若能,請給出相應的采購方案;若不能,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com