
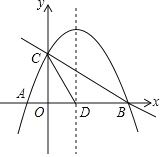
【題目】如圖,拋物線![]() 與x軸交于
與x軸交于![]() 、B兩點,與y軸交于點
、B兩點,與y軸交于點![]() ,拋物線的對稱軸交x軸于點D.
,拋物線的對稱軸交x軸于點D.
![]() 求拋物線的解析式;
求拋物線的解析式;
![]() 求
求![]() 的值;
的值;
![]() 在拋物線的對稱軸上是否存在點P,使
在拋物線的對稱軸上是否存在點P,使![]() 是以CD為腰的等腰三角形?如果存在,直接寫出點P的坐標;如果不存在,請說明理由;
是以CD為腰的等腰三角形?如果存在,直接寫出點P的坐標;如果不存在,請說明理由;
![]() 點E是線段BC上的一個動點,過點E作x軸的垂線與拋物線相交于點F,當點E運動到什么位置時線段EF最長?求出此時E點的坐標.
點E是線段BC上的一個動點,過點E作x軸的垂線與拋物線相交于點F,當點E運動到什么位置時線段EF最長?求出此時E點的坐標.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,點P的坐標為
;(3)存在,點P的坐標為![]() 或
或![]() ,
,![]() ,理由見解析;(4)當點E坐標為
,理由見解析;(4)當點E坐標為![]() 時,線段EF最長
時,線段EF最長
【解析】分析:(1)把點![]() ,
,![]() 代入到
代入到![]() ,用待定系數法,可得函數解析式;
,用待定系數法,可得函數解析式;
(2)根據勾股定理,可得BC的長,根據正弦函數的定義,可得答案;
(3)根據等腰三角形的定義,分PD=CD和PC=CD兩種情況可得P點坐標;
(4)根據平行于y軸的直線上兩點間的距離是較大的縱坐標減較小的縱坐標,可得二次函數,根據二次函數的性質,可得答案.
詳解:![]() 拋物線
拋物線![]() 過點
過點![]() ,
,![]() ,
,
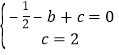
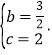
![]() 解析式為
解析式為![]() ,
,
![]() 當
當![]() 時,
時,![]() 解得
解得![]() 舍
舍![]() ,
,![]() ,
,
點B的坐標為![]() ,
,![]() ,
,
![]()
![]() .
.
![]() 存在.
存在.
![]() 對稱軸是
對稱軸是![]() ,
,
![]() 點D的坐標為
點D的坐標為![]() ,
,
![]() .
.
![]() ,得
,得![]() 或
或![]() ,
,
![]() ,即P點與D點關于底邊的高對稱,得
,即P點與D點關于底邊的高對稱,得
D點的縱坐標為4,即![]() ,
,
綜上所述:點P的坐標為![]() 或
或![]() ,
,![]() ;
;
![]() 設直線BC的解析式為
設直線BC的解析式為![]()
![]() 、C兩點坐標分別為
、C兩點坐標分別為![]() 、
、![]() ,
,
![]() 解得
解得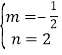 ,
,
![]() 直線BC的解析式為
直線BC的解析式為![]() .
.
設E點坐標為![]() ,則F點坐標為
,則F點坐標為![]() ,
,
![]()
![]()
![]() ,
,
當![]() 時,EF最長,
時,EF最長,
![]() 當點E坐標為
當點E坐標為![]() 時,線段EF最長.
時,線段EF最長.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】某校七、八年級各有學生400人,為了解這兩個年級普及安全教育的情況,進行了抽樣調查,過程如下
選擇樣本,收集數據從七、八年級各隨機抽取20名學生,進行安全教育考試,測試成績(百分制)如下:
七年級 85 79 89 83 89 98 68 89 79 59
99 87 85 89 97 86 89 90 89 77
八年級 71 94 87 92 55 94 98 78 86 94
62 99 94 51 88 97 94 98 85 91
分組整理,描述數據
(1)按如下頻數分布直方圖整理、描述這兩組樣本數據,請補全八年級20名學生安全教育頻數分布直方圖;

(2)兩組樣本數據的平均數、中位數、眾數、優秀率如下表所示,請補充完整;

得出結論,說明理由.
(3)整體成績較好的年級為___,理由為___(至少從兩個不同的角度說明合理性).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某網店以每件80元的進價購進某種商品,原來按每件100元的售價出售,一天可售出50件;后經市場調查,發現這種商品每件的售價每降低2元,其銷售量可增加10件.
(1)該網店銷售該商品原來一天可獲利潤 元.
(2)設后來該商品每件售價降價![]() 元,網店一天可獲利潤
元,網店一天可獲利潤![]() 元.
元.
①若此網店為了盡可能增加該商品的銷售量,且一天仍能獲利1080元,則每件商品的售價應降價多少元?
②求![]() 與
與![]() 之間的函數關系式,當該商品每件售價為多少元時,該網店一天所獲利潤最大?并求最大利潤值.
之間的函數關系式,當該商品每件售價為多少元時,該網店一天所獲利潤最大?并求最大利潤值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】1930年,德國漢堡大學的學生考拉茲,曾經提出過這樣一個數學猜想:對于每一個正整數,如果它是奇數,則對它乘3再加1;如果它是偶數,則對它除以2.如此循環,最終都能夠得到1.這一猜想后來成為著名的“考拉茲猜想”,又稱“奇偶歸一猜想”.雖然這個結論在數學上還沒有得到證明,但舉例驗證都是正確的,例如:取正整數5,最少經過下面5步運算可得1,即:![]() 如果正整數
如果正整數![]() 最少經過6步運算可得到1,則
最少經過6步運算可得到1,則![]() 的值為__________.
的值為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校決定加強羽毛球、籃球、乒乓球、排球、足球五項球類運動,每位同學必須且只能選擇一項球類運動,對該校學生隨機抽取![]() 進行調查,根據調查結果繪制了如圖不完整的頻數分布表和扇形統計圖:
進行調查,根據調查結果繪制了如圖不完整的頻數分布表和扇形統計圖:
運動項目 | 頻數 |
羽毛球 | 30 |
籃球 | a |
乒乓球 | 36 |
排球 | b |
足球 | 12 |
請根據以上圖表信息解答下列問題:
![]() 頻數分布表中的
頻數分布表中的![]() ______,
______,![]() ______;
______;
![]() 在扇形統計圖中,“排球”所在的扇形的圓心角為______度;
在扇形統計圖中,“排球”所在的扇形的圓心角為______度;
![]() 全校有多少名學生選擇參加乒乓球運動?
全校有多少名學生選擇參加乒乓球運動?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“切實減輕學生課業負擔”是我市作業改革的一項重要舉措.某中學為了解本校學生平均每天的課外學習時間情況,隨機抽取部分學生進行問卷調查,并將調查結果分為 A,B,C,D 四個等級.設學習時間為t(小時),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2 ,根據調查結果繪制了如圖所示的兩幅不完整的統計圖.請你根據圖中信息解答下列問題:
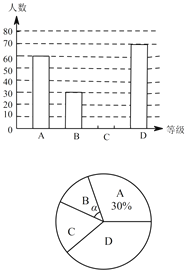
(1)該校共調查了多少名學生;
(2)將條形統計圖補充完整;
(3)求出表示 B等級的扇形圓心角 α 的度數;
(4)在此次問卷調查中,甲班有 2 人平均每天課外學習時間超過 2 小時,乙班有 3 人平均每天課外學習時間超過 2 小時,若從這 5 人中任選 2人去參加座談,試用列表或畫樹狀圖的方法求選出的2人
來自不同班級的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為實施鄉村振興戰略,解決某山區老百娃出行難的問題,當地政府決定修建一條高速公路,其中一段長為146米的山體隧道貫穿工程由甲、乙兩個工程隊負責施工,甲工程隊獨立工作2天后,乙工程隊加入,兩個工程隊又聯合工作了1天,這3天共掘進26米,已知甲工程隊平均每天比乙工程隊多掘進2米.
(1)求甲、乙兩個工程隊平均每天分別掘進多少米?
(2)若甲、乙兩個工程隊按此施工速度進行隧道貫穿工程,剩余工程由這兩個工程隊聯合施工,求完成這項隧道貫穿工程一共需要多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD內接于⊙O,AB=AD,對角線BD為⊙O的直徑,AC與BD交于點E.點F為CD延長線上,且DF=BC.
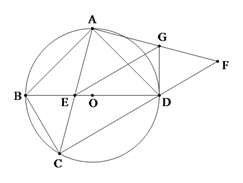
(1)證明:AC=AF;
(2)若AD=2,AF=![]() ,求AE的長;
,求AE的長;
(3)若EG∥CF交AF于點G,連接DG.證明:DG為⊙O的切線.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com