【題目】1930年，德國漢堡大學的學生考拉茲，曾經提出過這樣一個數學猜想：對于每一個正整數，如果它是奇數，則對它乘3再加1；如果它是偶數，則對它除以2．如此循環，最終都能夠得到1．這一猜想后來成為著名的“考拉茲猜想”，又稱“奇偶歸一猜想”．雖然這個結論在數學上還沒有得到證明，但舉例驗證都是正確的，例如：取正整數5，最少經過下面5步運算可得1，即：
如果正整數
最少經過6步運算可得到1，則的值為__________．
期末復習檢測系列答案
超能學典單元期中期末專題沖刺100分系列答案
黃岡360度定制密卷系列答案
陽光考場單元測試卷系列答案科目：初中數學 來源： 題型：
【題目】已知，數軸上點
在原點左邊，到原點的距離為8個單位長度，點
在原點的右邊，從點走到點，要經過32個單位長度．
（1）求、兩點所對應的數；
（2）若點
也是數軸上的點，點到點的距離是點到原點的距離的3倍，求點對應的數；
（3）已知，點
從點向右出發，速度為每秒1個單位長度，同時點
從點向右出發，速度為每秒2個單位長度，若點
到點的距離與點到原點
距離相等，則點到原點距離與點到點的距離與值是否變化？若不變，求其值．
查看答案和解析>>
科目：初中數學 來源： 題型：
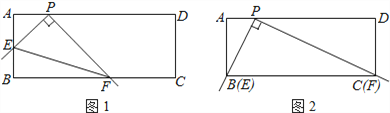
【題目】在矩形ABCD中，點P在AD上，AB=2，AP=1．將直角尺的頂點放在P處，直角尺的兩邊分別交AB，BC于點E，F，連接EF（如圖①）．
（1）當點E與點B重合時，點F恰好與點C重合（如圖②），求PC的長；
（2）探究：將直尺從圖②中的位置開始，繞點P順時針旋轉，當點E和點A重合時停止．在這個過程中，請你觀察、猜想，并解答：
①tan∠ PEF的值是否發生變化？請說明理由；
②直接寫出從開始到停止，線段EF的中點經過的路線長．
查看答案和解析>>
科目：初中數學 來源： 題型：
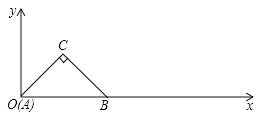
【題目】（3分）在Rt△ABC中，∠C=90°，AC=BC=1，將其放入平面直角坐標系，使A點與原點重合，AB在x軸上，△ABC沿x軸順時針無滑動的滾動，點A再次落在x軸時停止滾動，則點A經過的路線與x軸圍成圖形的面積為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為拓寬銷售渠道，某水果商店計劃將146個柚子和400個橙子裝入大、小兩種禮箱進行出售，其中每件小禮箱裝2個柚子和4個橙子；每件大禮箱裝3個柚子和9個橙子．要求每件禮箱都裝滿，柚子恰好全部裝完，橙子有剩余，設小禮箱的數量為x件.
（1）大禮箱的數量為________件(用含x的代數式表示).
（2）若橙子剩余12個，則需要大、小兩種禮箱共多少件?
（3）由于橙子有剩余，則小禮箱至少需要________件.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】綜合與實踐動手操作：用矩形下的折疊會出現等腰三角形，快速求BF的長．
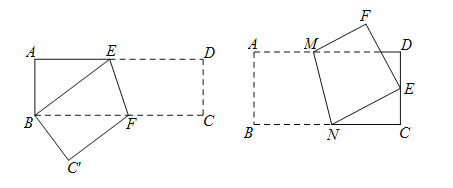
（1）如圖，在矩形ABCD中，AB=3，AD=9，將此矩形折疊，使點D與點B重合，折痕為EF，則等腰三角形是 ；
（2）利用勾股定理建立方程，求出BF的長是多少？
（3）拓展：將此矩形折疊，使點B與DC的中點E重合，請你利用添加輔助線的方法，求AM的長；
查看答案和解析>>
科目：初中數學 來源： 題型：
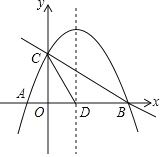
【題目】如圖，拋物線
與x軸交于
、B兩點，與y軸交于點
，拋物線的對稱軸交x軸于點D．
求拋物線的解析式；
求
的值；
在拋物線的對稱軸上是否存在點P，使
是以CD為腰的等腰三角形？如果存在，直接寫出點P的坐標；如果不存在，請說明理由；
點E是線段BC上的一個動點，過點E作x軸的垂線與拋物線相交于點F，當點E運動到什么位置時線段EF最長？求出此時E點的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知數軸上有
六個點，點
在原點位置，點
表示的數為
，已知下表中
的含義均為前一個點所表示的數與后一個點所表示的數的差，比如
為
．
|
|
|
|
|
|
|
|
|
|
若點
與點
的距離為
，則
的值為________
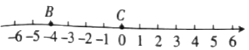
查看答案和解析>>
科目：初中數學 來源： 題型：
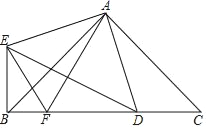
【題目】如圖，△ABC和△ADE分別是以BC，DE為底邊且頂角相等的等腰三角形，點D在線段BC上，AF平分DE交BC于點F，連接BE，EF．
（1）CD與BE相等？若相等，請證明；若不相等，請說明理由；
（2）若∠BAC=90°，求證：BF2+CD2=FD2．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
