
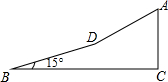
 如圖,某校八年級(1)班學生利用寒假期間到郊區進行社會實踐活動,活動之余,同學們準備攀登附近的一個小山坡,從B點出發,沿坡腳15°的坡面以5千米/時的速度行至D點,用了10分鐘,然后沿坡比為1:$\sqrt{3}$的坡面以3千米/時的速度達到山頂A點,用了5分鐘,求小山坡的高(即AC的長度)(精確到0.01千米)(sin15°≈0.2588,cos15°≈0.9659,$\sqrt{3}$≈1.732)
如圖,某校八年級(1)班學生利用寒假期間到郊區進行社會實踐活動,活動之余,同學們準備攀登附近的一個小山坡,從B點出發,沿坡腳15°的坡面以5千米/時的速度行至D點,用了10分鐘,然后沿坡比為1:$\sqrt{3}$的坡面以3千米/時的速度達到山頂A點,用了5分鐘,求小山坡的高(即AC的長度)(精確到0.01千米)(sin15°≈0.2588,cos15°≈0.9659,$\sqrt{3}$≈1.732) 分析 過點D作DF⊥BC于F,DE⊥AC于點E,分別利用坡角及三角函數求出AE,DF的值即可求得AC的長.
解答 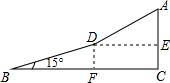 解:過D作DF⊥BC于F,DE⊥AC于點E,
解:過D作DF⊥BC于F,DE⊥AC于點E,
∵沿坡比為1:$\sqrt{3}$的坡面以3千米/時的速度達到山頂A點,
∴$\frac{AE}{DE}$=$\frac{1}{\sqrt{3}}$,
∴∠ADE=30°,
∵BD=$\frac{5}{60}$×10=$\frac{5}{6}$(km),AD=$\frac{3}{60}$×5=$\frac{1}{4}$(km),
∴AC=AE+EC=AE+DF=AD•sin30°+BD•sin15°=$\frac{1}{4}$×$\frac{1}{2}$+$\frac{5}{6}$×0.2588≈0.34(千米).
答:小山坡的高為0.34千米.
點評 此題主要考查了坡度坡角問題以及及三角函數的綜合運用,正確應用銳角三角函數關系是解題關鍵.


科目:初中數學 來源: 題型:選擇題
 如圖,平行四邊形ABCD的對角線AC、BD相交于點O,則下列說法一定正確的( )
如圖,平行四邊形ABCD的對角線AC、BD相交于點O,則下列說法一定正確的( )| A. | AO=OD | B. | AO⊥OD | C. | AO=OC | D. | AO⊥AB |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
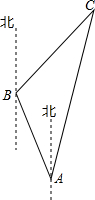 為有效開發海洋資源,保護海洋權益,我國對南海諸島進行了全面調查,一測量船在A島測得B島在北偏西30°,C島在北偏東15°,航行100海里到達B島,在B島測得C島在北偏東45°,求B,C兩島及A,C兩島的距離($\sqrt{6}$≈2.45,結果保留到整數)
為有效開發海洋資源,保護海洋權益,我國對南海諸島進行了全面調查,一測量船在A島測得B島在北偏西30°,C島在北偏東15°,航行100海里到達B島,在B島測得C島在北偏東45°,求B,C兩島及A,C兩島的距離($\sqrt{6}$≈2.45,結果保留到整數)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com