
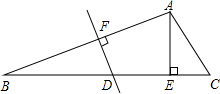
 如圖,△ABC中,∠C=60°,AB的垂直平分線交BC于點D,DE=6,BD=6$\sqrt{2}$,AE⊥BC于E,求EC的長.
如圖,△ABC中,∠C=60°,AB的垂直平分線交BC于點D,DE=6,BD=6$\sqrt{2}$,AE⊥BC于E,求EC的長. 分析 首先作出輔助線連接AD,再利用線段垂直平分線的性質計算.
解答 解:連接AD,
∵AB的垂直平分線交BC于點D,
∴BD=AD,
∵DE=6,BD=6$\sqrt{2}$,
∴AD=6$\sqrt{2}$,
∴∠ADE=45°,
∴∠B=22.5°,∵∠C=60°,
∴∠BAC=97.5°,
∵∠ADE=∠B+∠DAB=45°,AE⊥BC,
∴DE=AE=6,
∵∠C=60°,
∴∠CAE=90°-60°=30°,
∴AC=2CE,
在Rt△ACE中,AC2=AE2+CE2,
即4CE2=62+CE2,
∴CE2=12,
解得EC=2$\sqrt{3}$.
點評 本題考查了線段垂直平分線的性質,解直角三角形,本題關鍵是作出輔助線提示:連接AD.考查的是線段垂直平分線的性質(垂直平分線上任意一點,和線段兩端點的距離相等)有關知識.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com