
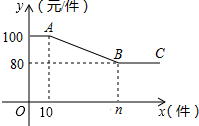
 小穎媽媽的網店加盟了“小神龍”童裝銷售,有一款童裝的進價為60元/件,售價為100元/件,因為剛加盟,為了增加銷量,準備對大客戶制定如下“促銷優惠”方案:
小穎媽媽的網店加盟了“小神龍”童裝銷售,有一款童裝的進價為60元/件,售價為100元/件,因為剛加盟,為了增加銷量,準備對大客戶制定如下“促銷優惠”方案:分析 (1)根據:實際售價=原售價-1×超過10的件數,可得;利用價格變化規律,進而求出n的值;
(2)分類討論:當0<x≤10時,當10<x≤30時;當x>30時,分別根據:總利潤=每件利潤×銷售量得出函數關系式;
(3)配方W=-x2+50x得到W=-(x-25)2+625,根據二次函數的性質討論增減性,即可知銷量越大利潤就越大時的最低售價.
解答 解:(1)一次購買20件這款童裝的售價為:100-(20-10)=90元/件,n=(100-80)+10=30,
故答案為:90,30;
(2)當0<x≤10時,w=(100-60)x=40x,
當10<x≤30時,∵y=100-(x-10)=110-x,
∴w=[100-(x-10)-60]x=-x2+50x,
當x>30時,w=(80-60)x=20x;
(3)當10<x≤30時,w=-x2+50x=-(x-25)2+625.
①當10<x≤25時,w隨x的增大而增大,即賣的個數越多,利潤越大.
②當25<x≤30時,w隨x的增大而減小,即賣的個數越多,利潤越小.
當x=25時,售價為y=110-x=85(元).
答:最低售價應定為85元/件.
點評 本題考查了二次函數的應用:先得到二次函數的頂點式y=a(x-h)2+k,當a<0,x=h時,y有最大值k;當a<0,x=h時,y有最小值k;也考查了二次函數的增減性,熟練的運用二次函數的增減性質是解決問題的關鍵.


 導學教程高中新課標系列答案
導學教程高中新課標系列答案科目:初中數學 來源: 題型:選擇題
| 成績(分) | 9.40 | 9.50 | 9.60 | 9.70 | 9.80 | 9.90 |
| 人數 | 2 | 3 | 5 | 4 | 3 | 1 |
| A. | 9.70,9.60 | B. | 9.60,9.60 | C. | 9.60,9.70 | D. | 9.65,9.60 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
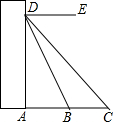 如圖,小明家所在住宅樓樓前廣場的寬AB為30米,線段BC為AB正前方的一條道路的寬.小明站在家里點D處觀察B,C兩點的俯角分別為60°和45°,已知DA垂直地面,則這條道路的寬BC為21.96米($\sqrt{3}$≈1.732)
如圖,小明家所在住宅樓樓前廣場的寬AB為30米,線段BC為AB正前方的一條道路的寬.小明站在家里點D處觀察B,C兩點的俯角分別為60°和45°,已知DA垂直地面,則這條道路的寬BC為21.96米($\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 現要建造一段鐵路,其路基的橫斷面ABCD是等腰梯形,上底CD=8米,高DH為2.5米,坡度i=1:1.2.
現要建造一段鐵路,其路基的橫斷面ABCD是等腰梯形,上底CD=8米,高DH為2.5米,坡度i=1:1.2.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com