
【題目】如圖1,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,它在平面直角坐標系中位置如圖所示,點
,它在平面直角坐標系中位置如圖所示,點![]() 在
在![]() 軸的負半軸上(點
軸的負半軸上(點![]() 在點
在點![]() 的右側),頂點
的右側),頂點![]() 在第二象限,將
在第二象限,將![]() 沿
沿![]() 所在的直線翻折,點
所在的直線翻折,點![]() 落在點
落在點![]() 位置
位置
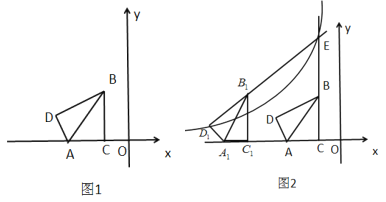
(1)若點![]() 坐標為
坐標為![]() 時,求點
時,求點![]() 的坐標;
的坐標;
(2)若點![]() 和點
和點![]() 在同一個反比例函數的圖象上,求點
在同一個反比例函數的圖象上,求點![]() 坐標;
坐標;
(3)如圖2,將四邊形![]() 向左平移,平移后的四邊形記作四邊形
向左平移,平移后的四邊形記作四邊形![]() ,過點
,過點![]() 的反比例函數
的反比例函數![]() 的圖象與
的圖象與![]() 的延長線交于點
的延長線交于點![]() ,則在平移過程中,是否存在這樣的
,則在平移過程中,是否存在這樣的![]() ,使得以點
,使得以點![]() 為頂點的三角形是直角三角形且點
為頂點的三角形是直角三角形且點![]() 在同一條直線上?若存在,求出
在同一條直線上?若存在,求出![]() 的值;若不存在,請說明理由
的值;若不存在,請說明理由
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() 或
或![]()
【解析】
(1)過點![]() 作
作![]() 軸于點
軸于點![]() ,利用三角函數值可得出
,利用三角函數值可得出![]() ,再根據翻折的性質可得出
,再根據翻折的性質可得出![]() ,
,![]() ,再解
,再解![]() ,得出
,得出![]() ,
,![]() ,最后結合點C的坐標即可得出答案;
,最后結合點C的坐標即可得出答案;
(2)設點![]() 坐標為
坐標為![]() (
(![]() ),則點
),則點![]() 的坐標是
的坐標是![]() ,利用(1)得出的結果作為已知條件,可得出點D的坐標為
,利用(1)得出的結果作為已知條件,可得出點D的坐標為![]() ,再結合反比例函數求解即可;
,再結合反比例函數求解即可;
(3)首先存在這樣的k值,分![]() 和
和![]() 兩種情況討論分析即可.
兩種情況討論分析即可.
解:(1)如圖,過點![]() 作
作![]() 軸于點
軸于點![]()
∵![]() ,
,
∴![]()
∴![]()
由題意可知![]() ,
,![]() .
.
∴![]() .
.
∴![]()
在![]() 中,
中,![]() ,
,
∴![]() ,
,![]() .
.
∵點![]() 坐標為
坐標為![]() ,
,
∴![]() .
.
∴點![]() 的坐標是
的坐標是![]()
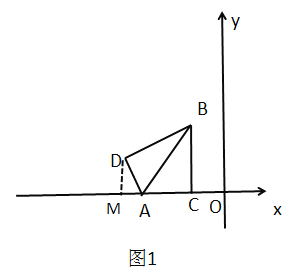
(2)設點![]() 坐標為
坐標為![]() (
(![]() ),則點
),則點![]() 的坐標是
的坐標是![]() ,
,
由(1)可知:點![]() 的坐標是
的坐標是![]()
∵點![]() 和點
和點![]() 在同一個反比例函數的圖象上,
在同一個反比例函數的圖象上,
∴![]() .解得
.解得![]() .
.
∴點![]() 坐標為
坐標為![]()
(3)存在這樣的![]() ,使得以點
,使得以點![]() ,
,![]() ,
,![]() 為頂點的三角形是直角三角形
為頂點的三角形是直角三角形
解:①當![]() 時.
時.
如圖所示,連接![]() ,
,![]() ,
,![]() ,
,![]() 與
與![]() 相交于點
相交于點![]() .
.
則![]() ,
,![]() ,
,![]() .
.
∴![]() ∽
∽![]()
∴![]()
∴![]()
又∵![]() ,
,
∴![]() ∽
∽![]() .
.
∴![]() ,
,![]() ,
,
∴![]() .
.
∴![]() ,
,![]()
設![]() (
(![]() ),則
),則![]() ,
,
∵![]() ,
,![]() 在同一反比例函數圖象上,
在同一反比例函數圖象上,
∴![]() .解得:
.解得:![]() .
.
∴![]()
∴![]()
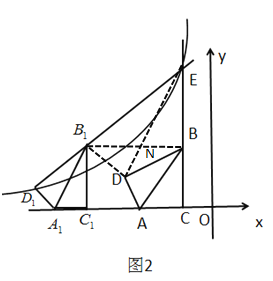
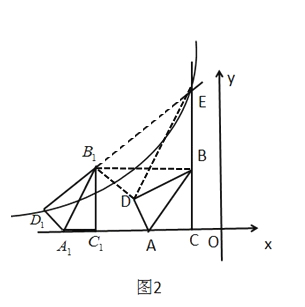
②當![]() 時.如圖所示,連接
時.如圖所示,連接![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() .
.
在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() .
.
在![]() 中,
中,
∵![]() ,
,
∴![]() .
.
∴![]()
設![]() (
(![]() ),則
),則![]()
∵![]() ,
,![]() 在同一反比例函數圖象上,
在同一反比例函數圖象上,
∴![]() .
.
解得:![]() ,
,
∴![]()
∴![]()


 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,將正方形![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 后得到正方形
后得到正方形![]() ,依此方式,繞點
,依此方式,繞點![]() 連續旋轉2019次得到正方形
連續旋轉2019次得到正方形![]() ,如果點
,如果點![]() 的坐標為(1,0),那么點
的坐標為(1,0),那么點![]() 的坐標為________.
的坐標為________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現如今,“垃圾分類”意識已深入人心,垃圾一般可分為:可回收物、廚余垃圾、有害垃圾、其它垃圾.其中甲拿了一袋垃圾,乙拿了兩袋垃圾.
(1)直接寫出甲所拿的垃圾恰好是“廚余垃圾”的概率;
(2)求乙所拿的兩袋垃圾不同類的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某化工廠要在規定時間內搬運1200噸化工原料.現有![]() ,
,![]() 兩種機器人可供選擇,已知
兩種機器人可供選擇,已知![]() 型機器人比
型機器人比![]() 型機器人每小時多搬運30噸型,
型機器人每小時多搬運30噸型,![]() 機器人搬運900噸所用的時間與
機器人搬運900噸所用的時間與![]() 型機器人搬運600噸所用的時間相等.
型機器人搬運600噸所用的時間相等.
(1)求兩種機器人每小時分別搬運多少噸化工原料.
(2)該工廠原計劃同時使用這兩種機器人搬運,工作一段時間后,![]() 型機器人又有了新的搬運任務需離開,但必須保證這批化工原料在11小時內全部搬運完畢.問
型機器人又有了新的搬運任務需離開,但必須保證這批化工原料在11小時內全部搬運完畢.問![]() 型機器人至少工作幾個小時,才能保證這批化工原料在規定的時間內完成?
型機器人至少工作幾個小時,才能保證這批化工原料在規定的時間內完成?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形AOBC放置在平面直角坐標系xOy中,邊OA在y軸的正半軸上,邊OB在x軸的正半軸上,拋物線的頂點為F,對稱軸交AC于點E,且拋物線經過點A(0,2),點C,點D(3,0).∠AOB的平分線是OE,交拋物線對稱軸左側于點H,連接HF.
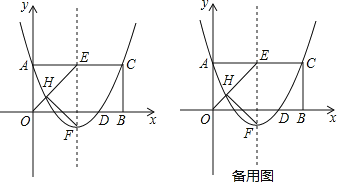
(1)求該拋物線的解析式;
(2)在x軸上有動點M,線段BC上有動點N,求四邊形EAMN的周長的最小值;
(3)該拋物線上是否存在點P,使得四邊形EHFP為平行四邊形?如果存在,求出點P的坐標;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)圖象如圖所示,下列結論:①abc>0;②2a+b=0;③a﹣b+c>0;④當x≠1時,a+b>ax2+bx;⑤4ac<b2.其中正確的有( )個
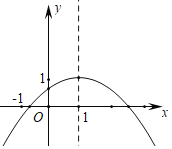
A.1個B.2個C.3個D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com