
 如圖,坡上有一顆與水平面EF垂直的大樹AB,臺風過后,大樹傾斜后折斷倒在山坡上,大樹頂部B接觸到坡面上的D點.已知山坡的坡角∠AEF=30°,量得樹干傾斜角∠BAC=45°,大樹被折斷部分和坡面所成的角∠ADC=60°且AD=4米.則這棵大樹折斷前的高度AB=(2$\sqrt{6}$+2$\sqrt{3}$+2)米.
如圖,坡上有一顆與水平面EF垂直的大樹AB,臺風過后,大樹傾斜后折斷倒在山坡上,大樹頂部B接觸到坡面上的D點.已知山坡的坡角∠AEF=30°,量得樹干傾斜角∠BAC=45°,大樹被折斷部分和坡面所成的角∠ADC=60°且AD=4米.則這棵大樹折斷前的高度AB=(2$\sqrt{6}$+2$\sqrt{3}$+2)米. 分析 過A作AM⊥CD于M,在直角三角形ADM中,求出∠DAM=30°,利用30度角所對的直角邊等于斜邊的一半求出AM與MD的長,確定出三角形ACM為等腰直角三角形,求出CM,AC的長,由AC+CM+MD求出大樹高即可.
解答 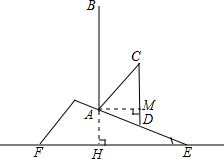 解:過A作AM⊥CD于M,
解:過A作AM⊥CD于M,
則AM=ADsin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,MD=$\frac{1}{2}$AD=2.
∵∠C=∠CAM=45°,
∴CM=AM=2$\sqrt{3}$,AC=$\sqrt{2}$AM=2$\sqrt{6}$,
∴AB=AC+CM+MD=2$\sqrt{6}$+2$\sqrt{3}$+2.
∴這棵大樹折斷前高度為(2$\sqrt{6}$+2$\sqrt{3}$+2)米.
點評 此題屬于解直角三角形的應用-坡度坡角問題,涉及的知識有:含30度角的直角三角形的性質,特殊角的三角函數值,等腰直角三角形的性質,熟練掌握性質及定理是解本題的關鍵.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:初中數學 來源:2016-2017學年廣東省佛山市順德區八年級3月月考數學試卷(解析版) 題型:單選題
已知關于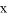 的方程
的方程 的解為負數,則m的取值范圍是( )
的解為負數,則m的取值范圍是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| 男生序號 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
| 身高x(cm) | 163 | 171 | 173 | 156 | 161 | 174 | 164 | 166 | 169 | 164 |
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2個 | B. | 3個 | C. | 4個 | D. | 5個 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 4個 | B. | 3個 | C. | 2個 | D. | 1個 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{16}$ | D. | $\frac{1}{27}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com