
【題目】第二十四屆冬季奧林匹克運動會將于2022年2月4日至2月20日在北京舉行,北京將成為歷史上第一座既舉辦過夏奧會又舉辦過冬奧會的城市.某區舉辦了一次冬奧知識網上答題競賽,甲、乙兩校各有![]() 名學生參加活動,為了解這兩所學校的成績情況,進行了抽樣調查,過程如下,請補充完整.
名學生參加活動,為了解這兩所學校的成績情況,進行了抽樣調查,過程如下,請補充完整.
[收集數據]
從甲、乙兩校各隨機抽取![]() 名學生,在這次競賽中他們的成績如下:
名學生,在這次競賽中他們的成績如下:
甲:![]()
![]()
乙:![]()
![]()
[整理、描述數據]按如下分數段整理、描述這兩組樣本數據:
學校 人數 成績 |
|
|
|
甲 |
|
|
|
乙 |
|
|
|
(說明:優秀成績為![]() ,良好成績為
,良好成績為![]() 合格成績為
合格成績為![]() .)
.)
[分析數據]兩組樣本數據的平均分、中位數、眾數如下表所示:
學校 | 平均分 | 中位數 | 眾數 |
甲 |
|
|
|
乙 |
|
|
|
其中![]() .
.
[得出結論]
(1)小明同學說:“這次競賽我得了![]() 分,在我們學校排名屬中游略偏上!”由表中數據可知小明是 _校的學生;(填“甲”或“乙”)
分,在我們學校排名屬中游略偏上!”由表中數據可知小明是 _校的學生;(填“甲”或“乙”)
(2)張老師從乙校隨機抽取--名學生的競賽成績,試估計這名學生的競賽成績為優秀的概率為_ ;
(3)根據以上數據推斷一所你認為競賽成績較好的學校,并說明理由: ;
(至少從兩個不同的角度說明推斷的合理性)
【答案】80;(1)甲;(2)![]() ;(3)乙學校競賽成績較好,理由見解析
;(3)乙學校競賽成績較好,理由見解析
【解析】
首先根據乙校的成績結合眾數的定義即可得出a的值;
(1)根據兩個學校成績的中位數進一步判斷即可;
(2)根據概率的定義,結合乙校優秀成績的概率進一步求解即可;
(3)根據題意,從平均數以及中位數兩方面加以比較分析即可.
由乙校成績可知,其中80出現的次數最多,故80為該組數據的眾數,∴a=80,
故答案為:80;
(1)由表格可知,甲校成績的中位數為60,乙校成績的中位數為75,
∵小明這次競賽得了![]() 分,在他們學校排名屬中游略偏上,
分,在他們學校排名屬中游略偏上,
∴小明為甲校學生,
故答案為:甲;
(2)乙校隨便抽取一名學生的成績,該學生成績為優秀的概率為:![]() ,
,
故答案為:![]() ;
;
(3)乙校競賽成績較好,理由如下:
因為乙校的平均分高于甲校的平均分說明平均水平高,乙校的中位數75高于甲校的中位數65,說明乙校分數不低于70分的學生比甲校多,綜上所述,乙校競賽成績較好.


科目:初中數學 來源: 題型:
【題目】青山區政府美化城市環境,計劃對面積為![]() 平方米的區域進行綠化,安排甲、乙兩個工程隊完成,已知乙隊每天能完成綠化的面積是甲隊每天能完成綠化面積的
平方米的區域進行綠化,安排甲、乙兩個工程隊完成,已知乙隊每天能完成綠化的面積是甲隊每天能完成綠化面積的![]() 倍,并且在獨立完成面積為平
倍,并且在獨立完成面積為平![]() 方米區域的綠化時,甲隊比乙隊多用
方米區域的綠化時,甲隊比乙隊多用![]() 天.
天.
![]() 求甲、乙兩工程隊每天能完成綠化的面積分別是多少平方米?
求甲、乙兩工程隊每天能完成綠化的面積分別是多少平方米?
![]() 若區政府每天需付給甲隊的綠化費用為
若區政府每天需付給甲隊的綠化費用為![]() 萬元,乙隊為
萬元,乙隊為![]() 萬元,要使這次的綠化總費用不超過
萬元,要使這次的綠化總費用不超過![]() 萬元,至少應安排甲隊工作多少天?
萬元,至少應安排甲隊工作多少天?
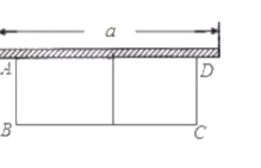
![]() 為合理利用綠化用地,這是需要用長為
為合理利用綠化用地,這是需要用長為![]() 米的植物隔離帶靠著墻(墻的最大可用長度為
米的植物隔離帶靠著墻(墻的最大可用長度為![]() 是
是![]() 米,植物隔離帶的自身寬度不計),如圖所示,圍成中間隔有植物隔離帶的長方形中央綠地,設綠地的寬
米,植物隔離帶的自身寬度不計),如圖所示,圍成中間隔有植物隔離帶的長方形中央綠地,設綠地的寬![]() 為
為![]() 米,面積為
米,面積為![]() 米
米![]() .試問中央綠地的面積能達到
.試問中央綠地的面積能達到![]() 嗎?如果能,請求出此時
嗎?如果能,請求出此時![]() 的長;如果不能,請說明理由.
的長;如果不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水產品養殖企業為指導該企業某種產品的養殖和銷售,對歷年市場行情和水產品的養殖情況進行了調查.調查發現這種水產品的每千克售價![]() (元)與銷售月份
(元)與銷售月份![]() (月)滿足關系式
(月)滿足關系式![]() +36,而其每千克成本
+36,而其每千克成本![]() (元)與銷售月份
(元)與銷售月份![]() (月)滿足的函數關系如圖所示:
(月)滿足的函數關系如圖所示:
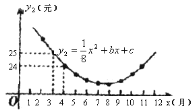
(1)試確定![]() 、
、![]() 的值;
的值;
(2)求出這種水產品每千克的利潤![]() (元)與銷售月份
(元)與銷售月份![]() (月)之間的函數關系式;
(月)之間的函數關系式;
(3)幾月份出售這種水產品每千克利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在平面直角坐標系中,拋物線y=ax2﹣2ax+4(a<0)交x軸于點A、B,與y軸交于點C,AB=6.
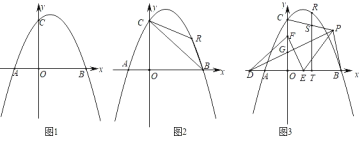
(1)如圖1,求拋物線的解析式;
(2)如圖2,點R為第一象限的拋物線上一點,分別連接RB、RC,設△RBC的面積為s,點R的橫坐標為t,求s與t的函數關系式;
(3)在(2)的條件下,如圖3,點D在x軸的負半軸上,點F在y軸的正半軸上,點E為OB上一點,點P為第一象限內一點,連接PD、EF,PD交OC于點G,DG=EF,PD⊥EF,連接PE,∠PEF=2∠PDE,連接PB、PC,過點R作RT⊥OB于點T,交PC于點S,若點P在BT的垂直平分線上,OB﹣TS=![]() ,求點R的坐標.
,求點R的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司共有![]() 三個部門,根據每個部門的員工人數和相應每人所創的年利潤繪制成如下的統計表和扇形圖.
三個部門,根據每個部門的員工人數和相應每人所創的年利潤繪制成如下的統計表和扇形圖.

各部門人數及每人所創年利潤統計表
部門 | 員工人數 | 每人所創的年利潤/萬元 |
A | 5 | 10 |
B |
| 8 |
C |
| 5 |
(1)①在扇形圖中,C部門所對應的圓心角的度數為___________;
②在統計表中,![]() ___________,
___________,![]() ___________;
___________;
(2)求這個公司平均每人所創年利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】張老師在講解復習《圓》的內容時,用投影儀屏幕展示出如下內容:
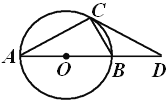
如圖,![]() 內接于
內接于![]() ,直徑
,直徑![]() 的長為2,過點
的長為2,過點![]() 的切線交
的切線交![]() 的延長線于點
的延長線于點![]() .
.
張老師讓同學們添加條件后,編制一道題目,并按要求完成下列填空.
(1)在屏幕內容中添加條件![]() ,則
,則![]() 的長為______.
的長為______.
(2)以下是小明、小聰的對話:
小明:我加的條件是![]() ,就可以求出
,就可以求出![]() 的長
的長
小聰:你這樣太簡單了,我加的是![]() ,連結
,連結![]() ,就可以證明
,就可以證明![]() 與
與![]() 全等.
全等.
參考上面對話,在屏幕內容中添加條件,編制一道題目(此題目不解答,可以添線、添字母).______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一輛汽車準備從甲地開往乙地.若平均速度為80km/h,則需要5h到達.
(1)寫出汽車從甲地到乙地所用時間![]() 與平均速度
與平均速度![]() 之間的關系式;
之間的關系式;
(2)如果準備用8h到達,那么平均速度是多少?
(3)已知汽車的最大平均速度是100km/h,那么汽車最少用多長時間可以到達?
查看答案和解析>>
科目:初中數學 來源: 題型:
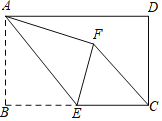
【題目】如圖,在矩形ABCD中,AB=4,BC=6,點E為BC的中點,將△ABE沿AE折疊,使點B落在矩形內的點F處,連接CF,則CF的長為(![]() )
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com