
【題目】青山區政府美化城市環境,計劃對面積為![]() 平方米的區域進行綠化,安排甲、乙兩個工程隊完成,已知乙隊每天能完成綠化的面積是甲隊每天能完成綠化面積的
平方米的區域進行綠化,安排甲、乙兩個工程隊完成,已知乙隊每天能完成綠化的面積是甲隊每天能完成綠化面積的![]() 倍,并且在獨立完成面積為平
倍,并且在獨立完成面積為平![]() 方米區域的綠化時,甲隊比乙隊多用
方米區域的綠化時,甲隊比乙隊多用![]() 天.
天.
![]() 求甲、乙兩工程隊每天能完成綠化的面積分別是多少平方米?
求甲、乙兩工程隊每天能完成綠化的面積分別是多少平方米?
![]() 若區政府每天需付給甲隊的綠化費用為
若區政府每天需付給甲隊的綠化費用為![]() 萬元,乙隊為
萬元,乙隊為![]() 萬元,要使這次的綠化總費用不超過
萬元,要使這次的綠化總費用不超過![]() 萬元,至少應安排甲隊工作多少天?
萬元,至少應安排甲隊工作多少天?
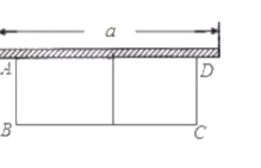
![]() 為合理利用綠化用地,這是需要用長為
為合理利用綠化用地,這是需要用長為![]() 米的植物隔離帶靠著墻(墻的最大可用長度為
米的植物隔離帶靠著墻(墻的最大可用長度為![]() 是
是![]() 米,植物隔離帶的自身寬度不計),如圖所示,圍成中間隔有植物隔離帶的長方形中央綠地,設綠地的寬
米,植物隔離帶的自身寬度不計),如圖所示,圍成中間隔有植物隔離帶的長方形中央綠地,設綠地的寬![]() 為
為![]() 米,面積為
米,面積為![]() 米
米![]() .試問中央綠地的面積能達到
.試問中央綠地的面積能達到![]() 嗎?如果能,請求出此時
嗎?如果能,請求出此時![]() 的長;如果不能,請說明理由.
的長;如果不能,請說明理由.
【答案】(1)甲工程隊每天能完成綠化的面積是![]() 平方米,乙工程隊每天能完成綠化的面積是
平方米,乙工程隊每天能完成綠化的面積是![]() 平方米;(2)至少應安排甲隊工作
平方米;(2)至少應安排甲隊工作![]() 天;(3)花圃的面積不能達到
天;(3)花圃的面積不能達到![]() ,理由詳見解析.
,理由詳見解析.
【解析】
(1)設甲工程隊每天能完成綠化的面積是x平方米,則乙工程隊每天能完成綠化的面積是1.5x平方米,根據工作時間=工作總量÷工作效率結合在獨立完成面積為450平方米區域的綠化時甲隊比乙隊多用5天,即可得出關于x的分式方程,解之經檢驗后即可得出結論;
(2)設安排甲隊工作m天,則需安排乙隊工作![]() 天,根據總費用=0.3×甲隊工作時間+0.9×乙隊工作時間結合這次的綠化總費用不超過24萬元,即可得出關于m的一元一次不等式,解之取其最小值即可得出結論;
天,根據總費用=0.3×甲隊工作時間+0.9×乙隊工作時間結合這次的綠化總費用不超過24萬元,即可得出關于m的一元一次不等式,解之取其最小值即可得出結論;
(3)求出中央綠地的面積為![]() ,根據二次函數的性質即可判斷.
,根據二次函數的性質即可判斷.
解:![]() 設甲工程隊每天能完成綠化的面積是
設甲工程隊每天能完成綠化的面積是![]() 平方米,
平方米,
則乙工程隊每天能完成綠化的面積是![]() 平方米,
平方米,
依題意,得: ![]() ,
,
解得:![]() ,
,
經檢驗,![]() 是原方程的解,且符合題意,
是原方程的解,且符合題意,
![]() .
.
答:甲工程隊每天能完成綠化的面積是![]() 平方米,乙工程隊每天能完成綠化的面積是
平方米,乙工程隊每天能完成綠化的面積是![]() 平方米.
平方米.
![]() 設安排甲隊工作
設安排甲隊工作![]() 天,則需安排乙隊工作
天,則需安排乙隊工作![]() 天,
天,
依題意,得:![]()
解得:![]() .
.
答:至少應安排甲隊工作![]() 天.
天.
![]() 中央綠地的面積為
中央綠地的面積為![]()
![]() 當
當![]() 長為
長為![]() ,寬為
,寬為![]() 時,有最大面積,為
時,有最大面積,為![]() 平方米
平方米
又![]() 當
當![]() 時,長方形中央綠地的長為
時,長方形中央綠地的長為![]() 米,
米,
又墻的最大可用長度![]() 是
是![]() ,故舍去;
,故舍去;
故花圃的面積不能達到![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
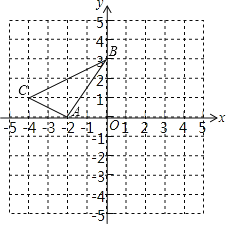
【題目】如圖,在平面直角坐標系xOy中,A(﹣2,0),B(0,3),C(﹣4,1).以原點O為旋轉中心,將△ABC順時針旋轉90°得到△A'B'C',其中點A,B,C旋轉后的對應點分別為點A',B',C'.
(1)畫出△A'B'C',并寫出點A',B',C'的坐標;
(2)求經過點B',B,A三點的拋物線對應的函數解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于給定的![]() ,我們給出如下定義:若點M是邊
,我們給出如下定義:若點M是邊![]() 上的一個定點,且以M為圓心的半圓上的所有點都在
上的一個定點,且以M為圓心的半圓上的所有點都在![]() 的內部或邊上,則稱這樣的半圓為
的內部或邊上,則稱這樣的半圓為![]() 邊上的點M關于
邊上的點M關于![]() 的內半圓,并將半徑最大的內半圓稱為點M關于
的內半圓,并將半徑最大的內半圓稱為點M關于![]() 的最大內半圓.若點M是邊
的最大內半圓.若點M是邊![]() 上的一個動點(M不與B,C重合),則在所有的點M關于
上的一個動點(M不與B,C重合),則在所有的點M關于![]() 的最大內半圓中,將半徑最大的內半圓稱為
的最大內半圓中,將半徑最大的內半圓稱為![]() 關于
關于![]() 的內半圓.
的內半圓.
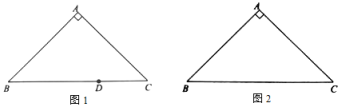
(1)在![]() 中,
中,![]() ,
,![]() ,
,
①如圖1,點D在邊![]() 上,且
上,且![]() ,直接寫出點D關于
,直接寫出點D關于![]() 的最大內半圓的半徑長;
的最大內半圓的半徑長;
②如圖2,畫出![]() 關于
關于![]() 的內半圓,并直接寫出它的半徑長;
的內半圓,并直接寫出它的半徑長;
(2)在平面直角坐標系![]() 中,點E的坐標為
中,點E的坐標為![]() ,點P在直線
,點P在直線![]() 上運動(P不與O重合),將
上運動(P不與O重合),將![]() 關于
關于![]() 的內半圓半徑記為R,當
的內半圓半徑記為R,當![]() 時,求點P的橫坐標t的取值范圍.
時,求點P的橫坐標t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商品經銷店欲購進A、B兩種紀念品,用320元購進的A種紀念品與用400元購進的B種紀念品的數量相同,每件B種紀念品的進價比A種紀念品的進價貴10元.
(1)求A、B兩種紀念品每件的進價分別為多少?
(2)若該商店A種紀念品每件售價45元,B種紀念品每件售價60元,這兩種紀念品共購進200件,這兩種紀念品全部售出后總獲利不低于1600元,求A種紀念品最多購進多少件.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點P在函數y=![]() (x>0)的圖象上從左向右運動,PA∥y軸,交函數y=﹣
(x>0)的圖象上從左向右運動,PA∥y軸,交函數y=﹣![]() (x>0)的圖象于點A,AB∥x軸交PO的延長線于點B,則△PAB的面積( )
(x>0)的圖象于點A,AB∥x軸交PO的延長線于點B,則△PAB的面積( )
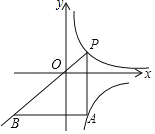
A.逐漸變大B.逐漸變小C.等于定值16D.等于定值24
查看答案和解析>>
科目:初中數學 來源: 題型:
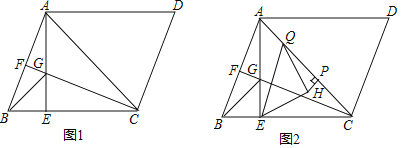
【題目】已知平行四邊形![]() ,過點
,過點![]() 作
作![]() 的垂線,垂足為點
的垂線,垂足為點![]() ,且滿足
,且滿足![]() ,過點
,過點![]() 作
作![]() 的垂線,垂足為點
的垂線,垂足為點![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() .
.
(1)如圖1,若![]() ,
,![]() ,求
,求![]() 的長度;
的長度;
(2)如圖2取![]() 上一點
上一點![]() ,連接
,連接![]() ,在
,在![]() 內取一點
內取一點![]() ,連接
,連接![]() ,
,![]() ,過點
,過點![]() 作
作![]() 的垂線,垂足為點
的垂線,垂足為點![]() ,若
,若![]() ,
,![]() .求證:
.求證:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
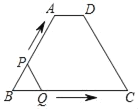
【題目】如圖,在四邊形ABCD中,AD∥BC,AB=CD,∠B=60°,AD=2,BC=8,點P從點B出發沿折線BA﹣AD﹣DC勻速運動,同時,點Q從點B出發沿折線BC﹣CD勻速運動,點P與點Q的速度相同,當二者相遇時,運動停止,設點P運動的路程為x,△BPQ的面積為y,則y關于x的函數圖象大致是( )
A.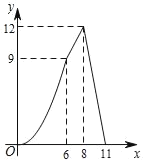 B.
B.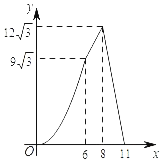
C.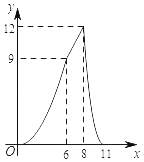 D.
D.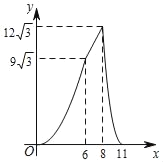
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】第二十四屆冬季奧林匹克運動會將于2022年2月4日至2月20日在北京舉行,北京將成為歷史上第一座既舉辦過夏奧會又舉辦過冬奧會的城市.某區舉辦了一次冬奧知識網上答題競賽,甲、乙兩校各有![]() 名學生參加活動,為了解這兩所學校的成績情況,進行了抽樣調查,過程如下,請補充完整.
名學生參加活動,為了解這兩所學校的成績情況,進行了抽樣調查,過程如下,請補充完整.
[收集數據]
從甲、乙兩校各隨機抽取![]() 名學生,在這次競賽中他們的成績如下:
名學生,在這次競賽中他們的成績如下:
甲:![]()
![]()
乙:![]()
![]()
[整理、描述數據]按如下分數段整理、描述這兩組樣本數據:
學校 人數 成績 |
|
|
|
甲 |
|
|
|
乙 |
|
|
|
(說明:優秀成績為![]() ,良好成績為
,良好成績為![]() 合格成績為
合格成績為![]() .)
.)
[分析數據]兩組樣本數據的平均分、中位數、眾數如下表所示:
學校 | 平均分 | 中位數 | 眾數 |
甲 |
|
|
|
乙 |
|
|
|
其中![]() .
.
[得出結論]
(1)小明同學說:“這次競賽我得了![]() 分,在我們學校排名屬中游略偏上!”由表中數據可知小明是 _校的學生;(填“甲”或“乙”)
分,在我們學校排名屬中游略偏上!”由表中數據可知小明是 _校的學生;(填“甲”或“乙”)
(2)張老師從乙校隨機抽取--名學生的競賽成績,試估計這名學生的競賽成績為優秀的概率為_ ;
(3)根據以上數據推斷一所你認為競賽成績較好的學校,并說明理由: ;
(至少從兩個不同的角度說明推斷的合理性)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com