
【題目】在平面直角坐標系xoy中,點A (-4,-2),將點A向右平移6個單位長度,得到點B.

(1)若拋物線y=-x2+bx+c經過點A,B,求此時拋物線的表達式;
(2)在(1)的條件下的拋物線頂點為C,點D是直線BC上一動點(不與B,C重合),是否存在點D,使△ABC和以點A,B,D構成的三角形相似?若存在,請求出此時D的坐標;若不存在,請說明理由;
(3)若拋物線y=-x2+bx+c的頂點在直線y=x+2上移動,當拋物線與線段![]() 有且只有一個公共點時,求拋物線頂點橫坐標t的取值范圍.
有且只有一個公共點時,求拋物線頂點橫坐標t的取值范圍.
【答案】(1)y=-x2-2x+6;(2)存在,D (![]() ,
,![]() );(3)-4≤t<-3或0<t≤5.
);(3)-4≤t<-3或0<t≤5.
【解析】
(1)根據點A的坐標結合線段AB的長度,可得出點B的坐標,根據點A,B的坐標,利用待定系數法即可求出拋物線的表達式;
(2)由拋物線解析式,求出頂點C的坐標,從而求出直線BC解析式,設D (d,-3d+4),
根據已知可知AD=AB=6時,△ABC∽△BAD,從而列出關于d的方程,解方程即可求解;
(3)將拋物線的表達式變形為頂點時,依此代入點A,B的坐標求出t的值,再結合圖形即可得出:當拋物線與線段AB有且只有一個公共點時t的取值范圍.
(1)∵點A的坐標為(-4,-2),將點A向右平移6個單位長度得到點B,
∴點B的坐標為(2,-2).
∵拋物線y=-x2+bx+c過點![]() ,
,
∴![]() , 解得
, 解得![]()
∴拋物線表達式為y=-x2-2x+6
(2)存在.
如圖
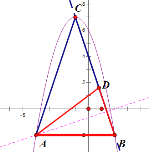
由(1)得,y=-x2-2x+6=-(x+1)2+7,
∴C (-1,7)
設直線BC解析式為y=kx+b
∴![]() 解之得,
解之得,![]()
∴lBC:y=-3x+4
設D (d,-3d+4),
∵在△ABC中AC=BC
∴當且僅當AD=AB=6時,兩三角形相似
即(-4-d)2+(-2+3d-4)2=36時,△ABC∽△BAD,
解之得,d1=![]() 、d2=2(舍去)
、d2=2(舍去)
∴存在點D,使△ABC和以點A,B,D構成的三角形相似,此時點D (![]() ,
,![]() );
);
(3)如圖:
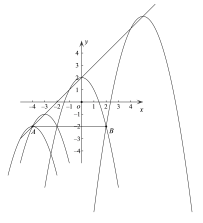
拋物線y=-x2+bx+c頂點在直線![]() 上
上
∴拋物線頂點坐標為![]()
∴拋物線表達式可化為![]() .
.
把![]() 代入表達式可得
代入表達式可得![]()
解得![]() .
.
又∵拋物線與線段AB有且只有一個公共點,
∴-4≤t<-3.
把![]() 代入表達式可得
代入表達式可得![]() .
.
解得![]() ,
,
又∵拋物線與線段AB有且只有一個公共點,
∴0<t≤5.
綜上可知![]() 的取值范圍時-4≤t<-3或0<t≤5.
的取值范圍時-4≤t<-3或0<t≤5.


科目:初中數學 來源: 題型:
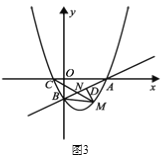
【題目】如圖![]() 所示,在平面直角坐標系
所示,在平面直角坐標系![]() 中,直線
中,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,拋物線
,拋物線![]() 經過
經過![]() ,
,![]() 兩點,與
兩點,與![]() 軸的另一交點為點
軸的另一交點為點![]() .
.
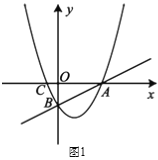
(1)求拋物線的函數表達式;
(2)點![]() 為直線
為直線![]() 下方拋物線上一動點.
下方拋物線上一動點.
①如圖2所示,直線![]() 交線段
交線段![]() 于點
于點![]() ,求
,求![]() 的最小值;
的最小值;
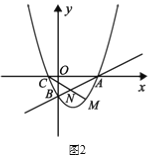
② 如圖3所示,連接![]() 過點
過點![]() 作
作![]() 于
于![]() ,是否存在點
,是否存在點![]() ,使得
,使得![]() 中的某個角恰好等于
中的某個角恰好等于![]() 的2倍?若存在,求點
的2倍?若存在,求點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一個直角三角形紙片![]() ,放置在平面直角坐標系中,點
,放置在平面直角坐標系中,點![]() ,點
,點![]() ,點
,點![]()
(I)過邊![]() 上的動點
上的動點![]() (點
(點![]() 不與點
不與點![]() ,
,![]() 重合)作
重合)作![]() 交
交![]() 于點
于點![]() ,沿著
,沿著![]() 折疊該紙片,點
折疊該紙片,點![]() 落在射線
落在射線![]() 上的點
上的點![]() 處.
處.
①如圖,當![]() 為
為![]() 中點時,求
中點時,求![]() 點的坐標;
點的坐標;
②連接![]() ,當
,當![]() 為直角三角形時,求
為直角三角形時,求![]() 點坐標:
點坐標:
(Ⅱ)![]() 是
是![]() 邊上的動點(點
邊上的動點(點![]() 不與點
不與點![]() 重合),將
重合),將![]() 沿
沿![]() 所在的直線折疊,得到
所在的直線折疊,得到![]() ,連接
,連接![]() ,當
,當![]() 取得最小值時,求
取得最小值時,求![]() 點坐標(直接寫出結果即可).
點坐標(直接寫出結果即可).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點A(﹣3,y1),B(2,y2)均在拋物線y=ax2+bx+c上,點P(m,n)是該拋物線的頂點,若y1>y2≥n,則m的取值范圍是( )
A.﹣3<m<2B.﹣![]() <m<-
<m<-![]() C.m>﹣
C.m>﹣![]() D.m>2
D.m>2
查看答案和解析>>
科目:初中數學 來源: 題型:
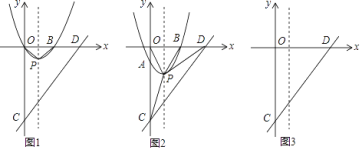
【題目】如圖1,拋物線y=![]() (x﹣m)2的頂點A在x軸正半軸上,交y軸于B點,S△OAB=1.
(x﹣m)2的頂點A在x軸正半軸上,交y軸于B點,S△OAB=1.

(1)求拋物線的解析式;
(2)如圖2,P是第一象限內拋物線上對稱軸右側一點,過P的直線l與拋物線有且只有一個公共點,l交拋物線對稱軸于C點,連PB交對稱軸于D點,若∠BAO=∠PCD,求證:AC=2AD;
(3)如圖3,以A為頂點作直角,直角邊分別與拋物線交于M、N兩點,當直角∠MAN繞A點旋轉時,求證:MN始終經過一個定點,并求出該定點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一矩形紙片![]() 放在直角坐標系中,
放在直角坐標系中,![]() 為原點,
為原點,![]() 在
在![]() 軸上,
軸上,![]() ,
,![]() .
.
(1)如圖①,在![]() 上取一點
上取一點![]() ,將
,將![]() 沿
沿![]() 折疊,使點
折疊,使點![]() 落在
落在![]() 邊上的
邊上的![]() 點,求
點,求![]() 點的坐標;
點的坐標;
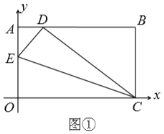
(2)如圖②,在![]() 、
、![]() 邊上選取適當的點
邊上選取適當的點![]() 、
、![]() ,將
,將![]() 沿
沿![]() 折疊,使
折疊,使![]() 點落在
點落在![]() 邊上
邊上![]() 點,過
點,過![]() 作
作![]() 交
交![]() 于
于![]() 點,交
點,交![]() 于
于![]() 點,設
點,設![]() 的坐標為
的坐標為![]() ,求
,求![]() 與
與![]() 之間的函數關系式,并直接寫出自變量
之間的函數關系式,并直接寫出自變量![]() 的取值范圍;
的取值范圍;

(3)在(2)的條件下,若![]() ,求
,求![]() 的面積.(直接寫出結果即可)
的面積.(直接寫出結果即可)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中, ![]() 是直線
是直線![]() 上的一點,連接
上的一點,連接![]() 過點
過點![]() 作
作![]() 交直線
交直線![]() 于點
于點![]() .
.
![]() 當點
當點![]() 在線段
在線段![]() 上時,如圖①,求證:
上時,如圖①,求證:![]() ;
;
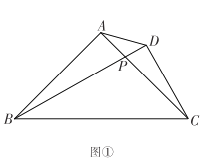
![]() 當點
當點![]() 在直線
在直線![]() 上移動時,位置如圖②、圖③所示,線段
上移動時,位置如圖②、圖③所示,線段![]() 與
與![]() 之間又有怎樣的數量關系?請直接寫出你的猜想,不需證明.
之間又有怎樣的數量關系?請直接寫出你的猜想,不需證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面直角坐標系中,拋物線y=x2﹣2x與x軸交于O、B兩點,頂點為P,連接OP、BP,直線y=x﹣4與y軸交于點C,與x軸交于點D.
(1)寫出點B坐標;判斷△OBP的形狀;
(2)將拋物線沿對稱軸平移m個單位長度,平移的過程中交y軸于點A,分別連接CP、DP;
(i)若拋物線向下平移m個單位長度,當S△PCD= ![]() S△POC時,求平移后的拋物線的頂點坐標;
S△POC時,求平移后的拋物線的頂點坐標;
(ii)在平移過程中,試探究S△PCD和S△POD之間的數量關系,直接寫出它們之間的數量關系及對應的m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△BCE中,點A是邊BE上一點,以AB為直徑的⊙O與CE相切于點D,AD∥OC,點F為OC與⊙O的交點,連接AF.
(1)求證:CB是⊙O的切線;
(2)若∠ECB=60°,AB=6,求圖中陰影部分的面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com