
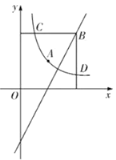
【題目】將一個直角三角形紙片![]() ,放置在平面直角坐標(biāo)系中,點
,放置在平面直角坐標(biāo)系中,點![]() ,點
,點![]() ,點
,點![]()
(I)過邊![]() 上的動點
上的動點![]() (點
(點![]() 不與點
不與點![]() ,
,![]() 重合)作
重合)作![]() 交
交![]() 于點
于點![]() ,沿著
,沿著![]() 折疊該紙片,點
折疊該紙片,點![]() 落在射線
落在射線![]() 上的點
上的點![]() 處.
處.
①如圖,當(dāng)![]() 為
為![]() 中點時,求
中點時,求![]() 點的坐標(biāo);
點的坐標(biāo);
②連接![]() ,當(dāng)
,當(dāng)![]() 為直角三角形時,求
為直角三角形時,求![]() 點坐標(biāo):
點坐標(biāo):
(Ⅱ)![]() 是
是![]() 邊上的動點(點
邊上的動點(點![]() 不與點
不與點![]() 重合),將
重合),將![]() 沿
沿![]() 所在的直線折疊,得到
所在的直線折疊,得到![]() ,連接
,連接![]() ,當(dāng)
,當(dāng)![]() 取得最小值時,求
取得最小值時,求![]() 點坐標(biāo)(直接寫出結(jié)果即可).
點坐標(biāo)(直接寫出結(jié)果即可).

【答案】(I)①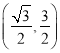 ;②
;②![]() 點坐標(biāo)為
點坐標(biāo)為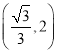 或
或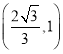 ;(II)
;(II)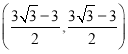
【解析】
(I)①過點E做EH⊥OA ,交OA于點H,由D為OB中點結(jié)合DE∥OA,可得出DE為△BOA的中位線,再根據(jù)點A、B的坐標(biāo)即可得出點E的坐標(biāo);
②根據(jù)折疊的性質(zhì)結(jié)合角的計算可得出∠AEF=60°≠90°,分∠AFE=90°和∠EAF=90°兩種情況考慮,利用含30度角的直角三角形以及勾股定理即可求出點E的坐標(biāo);
(II)根據(jù)三角形的三邊關(guān)系,找出當(dāng)點A′在y軸上時,BA′取最小值,根據(jù)折疊的性質(zhì)可得出直線OP的解析式,再根據(jù)點A、B的坐標(biāo)利用待定系數(shù)法求出直線AB的解析式,聯(lián)立兩直線解析式成方程組,解之即可得出點P的坐標(biāo).
(I)過點E做EH⊥OA ,交OA于點H,

①∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() 為
為![]() 中點,
中點,
∴D點的坐標(biāo)為![]() ,
,
∴![]() 為
為![]() 的中位線,
的中位線,
∴點![]() 為線段
為線段![]() 的中點,
的中點,
又∵![]() ,
,
∴EH為![]() 的中位線,
的中位線,
∴點H為線段OA的中點,
∴點H的坐標(biāo)為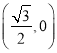 ,
,
∴點![]() 的坐標(biāo)為
的坐標(biāo)為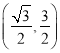 .
.
②∵點![]() ,點
,點![]() ,
,
∴![]() ,OB=3
,OB=3
∴![]() ,
,
∴∠B=30°,
由折疊可知:![]() .
.
∴![]() ,
,![]()
∴![]() .
.
∵![]() 是直角三角形,
是直角三角形,
∴![]() 或
或![]()
(i)當(dāng)![]() 時,如圖1所示
時,如圖1所示
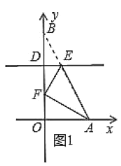
![]() .
.
在![]() 中,
中,![]() ,
,![]()
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,![]() .
.
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() .
.
∵![]() .
.
∴點![]() 的坐標(biāo)為
的坐標(biāo)為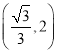 ;
;
(ii)當(dāng)![]() 時,如圖2所示.
時,如圖2所示.

∵![]() ,
,![]()
∴![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴點![]() 的坐標(biāo)為
的坐標(biāo)為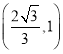 .
.
綜上所述:當(dāng)![]() 為直角三角形時,
為直角三角形時,![]() 點坐標(biāo)為
點坐標(biāo)為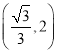 或
或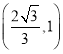 .
.
(II)由折疊可知:![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴當(dāng)點![]() 在
在![]() 軸上時,
軸上時,![]() 取最小值,如圖3所示.
取最小值,如圖3所示.
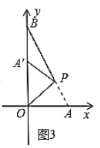
∵![]()
∴![]()
∴直線![]() 的解析式為
的解析式為![]()
設(shè)直線![]() 的解析式為
的解析式為![]() ,
,
將![]() 、
、![]() 代入
代入![]() 中,
中,
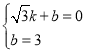 ,解得:
,解得: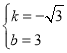 ,
,
∴直線![]() 的解忻式為
的解忻式為![]() .
.
聯(lián)立直線![]() 、
、![]() 的解析式成方程組,
的解析式成方程組,
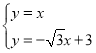 ,解得:
,解得: ,
,
∴.當(dāng)![]() 取得最小值時,
取得最小值時,![]() 點坐標(biāo)為
點坐標(biāo)為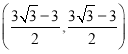 .
.


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案科目:初中數(shù)學(xué) 來源: 題型:
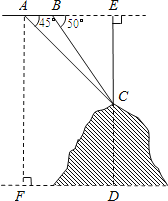
【題目】如圖,某飛機(jī)于空中探測某座山的高度,在點A處飛機(jī)的飛行高度是AF=3700米,從飛機(jī)上觀測山頂目標(biāo)C的俯角是45°,飛機(jī)繼續(xù)以相同的高度飛行300米到B處,此時觀測目標(biāo)C的俯角是50°,求這座山的高度CD.(參考數(shù)據(jù):sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,直線AB和拋物線的交點是A(0,-3),B(5,9),已知拋物線的頂點D的橫坐標(biāo)是2.
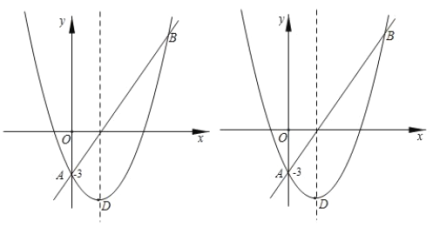
(1)求拋物線的解析式及頂點坐標(biāo);
(2)在![]() 軸上是否存在一點C,與A,B組成等腰三角形?若存在,求出點C的坐標(biāo),若不存在,請說明理由;
軸上是否存在一點C,與A,B組成等腰三角形?若存在,求出點C的坐標(biāo),若不存在,請說明理由;
(3)在直線AB的下方拋物線上找一點P,連接PA,PB使得△PAB的面積最大,并求出這個最大值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
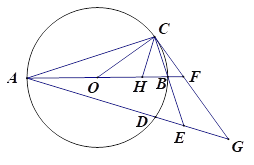
【題目】如圖,已知AB為⊙O的直徑,AB=8,點C和點D是⊙O上關(guān)于直線AB對稱的兩個點,連接OC、AC,且∠BOC<90°,直線BC和直線AD相交于點E,過點C作直線CG與線段AB的延長線相交于點F,與直線AD相交于點G,且∠GAF=∠GCE
(1)求證:直線CG為⊙O的切線;
(2)若點H為線段OB上一點,連接CH,滿足CB=CH,
①△CBH∽△OBC
②求OH+HC的最大值
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
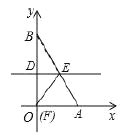
【題目】將一個直角三角形紙片![]() ,放置在平面直角坐標(biāo)系中,點
,放置在平面直角坐標(biāo)系中,點![]() ,點
,點![]() ,點
,點![]()
(I)過邊![]() 上的動點
上的動點![]() (點
(點![]() 不與點
不與點![]() ,
,![]() 重合)作
重合)作![]() 交
交![]() 于點
于點![]() ,沿著
,沿著![]() 折疊該紙片,點
折疊該紙片,點![]() 落在射線
落在射線![]() 上的點
上的點![]() 處.
處.
①如圖,當(dāng)![]() 為
為![]() 中點時,求
中點時,求![]() 點的坐標(biāo);
點的坐標(biāo);
②連接![]() ,當(dāng)
,當(dāng)![]() 為直角三角形時,求
為直角三角形時,求![]() 點坐標(biāo):
點坐標(biāo):
(Ⅱ)![]() 是
是![]() 邊上的動點(點
邊上的動點(點![]() 不與點
不與點![]() 重合),將
重合),將![]() 沿
沿![]() 所在的直線折疊,得到
所在的直線折疊,得到![]() ,連接
,連接![]() ,當(dāng)
,當(dāng)![]() 取得最小值時,求
取得最小值時,求![]() 點坐標(biāo)(直接寫出結(jié)果即可).
點坐標(biāo)(直接寫出結(jié)果即可).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】課外閱讀是提高學(xué)生素養(yǎng)的重要途徑.某校為了解本校學(xué)生課外閱讀情況,對九年級學(xué)生進(jìn)行隨機(jī)抽樣調(diào)查.如圖是根據(jù)調(diào)查結(jié)果繪制成的統(tǒng)計圖(不完整),請根據(jù)圖中提供的信息,解答下面的問題:
(1)本次抽樣調(diào)查的樣本容量是____ ____;
(2)在條形統(tǒng)計圖補(bǔ)中,計算出日人均閱讀時間在0.5~1小時的人數(shù)是____ ____,并將條形統(tǒng)計圖補(bǔ)充完整;
(3)在扇形統(tǒng)計圖中,計算出日人均閱讀時間在1~1.5小時對應(yīng)的圓心角度數(shù)____ ____度;
(4)根據(jù)本次抽樣調(diào)查,試估計該市15000名九年級學(xué)生中日人均閱讀時間在0.5~1.5小時的人數(shù).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】對于下列結(jié)論:
①二次函數(shù)![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() 隨
隨![]() 的增大而增大.
的增大而增大.
②關(guān)于![]() 的方程
的方程![]() 的解是
的解是![]() ,
,![]() (
(![]() 、
、![]() 、
、![]() 均為常數(shù),
均為常數(shù),![]() ),則方程
),則方程![]() 的解是
的解是![]() ,
,![]() .
.
③設(shè)二次函數(shù)![]() ,當(dāng)
,當(dāng)![]() 時,總有
時,總有![]() ,當(dāng)
,當(dāng)![]() 時,總有
時,總有![]() ,那么
,那么![]() 的取值范圍是
的取值范圍是![]() .
.
其中,正確結(jié)論的個數(shù)是( )
A.0個B.1個C.2個D.3個
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xoy中,點A (-4,-2),將點A向右平移6個單位長度,得到點B.

(1)若拋物線y=-x2+bx+c經(jīng)過點A,B,求此時拋物線的表達(dá)式;
(2)在(1)的條件下的拋物線頂點為C,點D是直線BC上一動點(不與B,C重合),是否存在點D,使△ABC和以點A,B,D構(gòu)成的三角形相似?若存在,請求出此時D的坐標(biāo);若不存在,請說明理由;
(3)若拋物線y=-x2+bx+c的頂點在直線y=x+2上移動,當(dāng)拋物線與線段![]() 有且只有一個公共點時,求拋物線頂點橫坐標(biāo)t的取值范圍.
有且只有一個公共點時,求拋物線頂點橫坐標(biāo)t的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,我們定義:橫坐標(biāo)與縱坐標(biāo)均為整數(shù)的點為整點如圖,已知雙曲線![]() 經(jīng)過點
經(jīng)過點![]() ,記雙曲線與兩坐標(biāo)軸之間的部分為
,記雙曲線與兩坐標(biāo)軸之間的部分為![]() (不含雙曲線與坐標(biāo)軸).
(不含雙曲線與坐標(biāo)軸).
(1)求![]() 的值;
的值;
(2)求![]() 內(nèi)整點的個數(shù);
內(nèi)整點的個數(shù);
(3)設(shè)點![]() 在直線
在直線![]() 上,過點
上,過點![]() 分別作平行于
分別作平行于![]() 軸
軸![]() 軸的直線,交雙曲線
軸的直線,交雙曲線![]()
![]() 于點
于點![]() ,記線段
,記線段![]() 、雙曲線所圍成的區(qū)域為
、雙曲線所圍成的區(qū)域為![]() ,若
,若![]() 內(nèi)部(不包括邊界)不超過
內(nèi)部(不包括邊界)不超過![]() 個整點,求
個整點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com