
【題目】如圖,已知在正方形![]() 中,對(duì)角線
中,對(duì)角線![]() 與
與![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,
,![]() ,
,![]() 分別是
分別是![]() 與
與![]() 的平分線,
的平分線,![]() 的延長(zhǎng)線與
的延長(zhǎng)線與![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,則下列結(jié)論:①
,則下列結(jié)論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正確的結(jié)論是( )
.其中正確的結(jié)論是( )
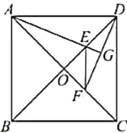
A.①②B.③④C.①②③D.①②③④
【答案】C
【解析】
由正方形的性質(zhì)可得∠ACD=∠ADB=45°,根據(jù)三角形外角性質(zhì)及角平分線的定義可得∠AFD=∠ADF,可證明AF=AD,根據(jù)等腰三角形“三線合一”的性質(zhì)可得AG⊥DF,可得AG為DF的垂直平分線,可判定①正確;根據(jù)垂直平分線的性質(zhì)可得EF=ED,可得∠EFD=∠EDF,即可證明∠EFD=∠FDC,可得EF//CD,即可證明EF//AB,可判定②正確;根據(jù)正方形的性質(zhì)可得AB=AD,即可證明AB=AF,可判定③正確,由EF=ED,EF為Rt△EOF的斜邊,可得ED>OE,即可得出EF不是△OCD的中位線,可得CD≠2EF,根據(jù)AB=CD即可判定④錯(cuò)誤;綜上即可得答案.
∵在正方形![]() 中,對(duì)角線
中,對(duì)角線![]() 與
與![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,
,
∴∠ACD=∠ADB=45°,∠DOC=90°,AB=AD,
∵DF為∠ODC的平分線,
∴∠ODF=∠CDF,
∴∠ADB+∠ODF=∠ACD+∠CDF,即∠AFD=∠ADF,
∴AD=AF,
∵AG為∠OAD的平分線,
∴AG⊥DF,故①正確,
∴AG為DF的垂直平分線,
∴ED=EF,
∴∠EFD=∠EDF,
∴∠EFD=∠CDF,
∴EF//CD,
∵AB//CD,
∴EF//AB,故②正確,
∵AD=AB,AD=AF,
∴AB=AF,故③正確,
∵EF=ED,EF為Rt△EOF的斜邊,
∴ED>OE,
∵EF//CD,
∴EF不是△OCD的中位線,
∴CD≠2EF,即AB≠2EF,故④錯(cuò)誤,
綜上所述:正確的結(jié)論有①②③,
故選:C.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
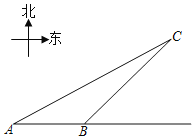
【題目】如圖,我市某景區(qū)內(nèi)有一條自西向東的筆直林蔭路經(jīng)過(guò)景點(diǎn)A、B,現(xiàn)市政決定開(kāi)發(fā)景點(diǎn)C,經(jīng)考察人員測(cè)量,景點(diǎn)A位于景點(diǎn)C的在南偏西60°方向,景點(diǎn)B位于景點(diǎn)C的西南方向,A、B兩景點(diǎn)之間相距380米,現(xiàn)準(zhǔn)備由景點(diǎn)C向該林萌路修建一條距離最短的公路,不考慮其它因素,求出這條公路的長(zhǎng)?(結(jié)果精確到0.1,參考數(shù)據(jù):![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
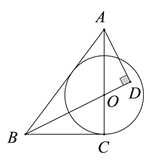
【題目】如圖,在![]() 中,
中,![]() 為
為![]() 上一點(diǎn),以
上一點(diǎn),以![]() 為圓心,
為圓心,![]() 長(zhǎng)為半徑作圓,與
長(zhǎng)為半徑作圓,與![]() 相切于點(diǎn)
相切于點(diǎn)![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 作
作![]() 交
交![]() 的延長(zhǎng)線于點(diǎn)
的延長(zhǎng)線于點(diǎn)![]() ,且
,且![]() .
.
(1)求證:![]() 為
為![]() 的切線;
的切線;
(2)若![]() ,
,![]() ,求
,求![]() 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
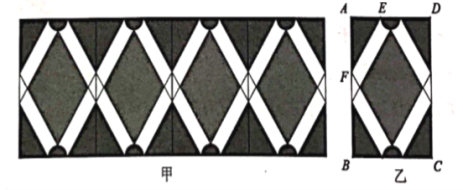
【題目】圖甲是小明設(shè)計(jì)的花邊圖案作品該作品由形如圖乙的矩形圖案拼接而成(不重疊,無(wú)縫隙).該矩形圖案既是軸對(duì)稱圖形,又是中心對(duì)稱圖形.圖乙中,![]() ,上、下兩個(gè)半圓的面積之和為
,上、下兩個(gè)半圓的面積之和為![]() ,中間陰影菱形的一組對(duì)邊與
,中間陰影菱形的一組對(duì)邊與![]() 平行,且菱形的面積比
平行,且菱形的面積比![]() 個(gè)角上的陰影三角形的面積之和大
個(gè)角上的陰影三角形的面積之和大![]() ,則
,則![]() 的長(zhǎng)度為__________
的長(zhǎng)度為__________![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】為實(shí)現(xiàn)2020年全面脫貧的目標(biāo),我國(guó)實(shí)施“精準(zhǔn)扶貧”戰(zhàn)略,從而使貧困戶的生活條件得到改善,生活質(zhì)量明顯提高.為了切實(shí)關(guān)注、關(guān)愛(ài)貧困家庭學(xué)生,某校對(duì)全校各班貧困家庭學(xué)生的人數(shù)情況進(jìn)行了統(tǒng)計(jì),統(tǒng)計(jì)發(fā)現(xiàn)班上貧困家庭學(xué)生人數(shù)分別有2名,3名,4名,5名,6名,共五種情況.并將其制成了如下兩幅不完整的統(tǒng)計(jì)圖:

請(qǐng)回答下列問(wèn)題:
(1)求該校一共有班級(jí)________個(gè);在扇形統(tǒng)計(jì)圖中,貧困家庭學(xué)生人數(shù)有5名的班級(jí)所對(duì)應(yīng)扇形圓心角為________°;
(2)將條形圖補(bǔ)充完整;
(3)甲、乙、丙是貧困生中的三名學(xué)生,學(xué)校決定從這三名學(xué)生中隨機(jī)抽取兩名代表到市里進(jìn)行發(fā)言,用列表法或畫(huà)樹(shù)狀圖法,求同時(shí)抽到甲,乙兩名學(xué)生的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,點(diǎn)![]() 為坐標(biāo)原點(diǎn),拋物線
為坐標(biāo)原點(diǎn),拋物線![]() 交
交![]() 軸于
軸于![]() 、
、![]() (
(![]() 左
左![]() 右)兩點(diǎn),交
右)兩點(diǎn),交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,
,![]() ,
,![]() .
.
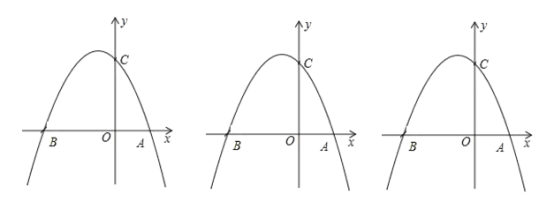
(1)求拋物線的解析式;
(2)點(diǎn)![]() 為第二象限拋物線上一點(diǎn),連接
為第二象限拋物線上一點(diǎn),連接![]() 、
、![]() ,
,![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 做
做![]() 軸的垂線,垂足為點(diǎn)
軸的垂線,垂足為點(diǎn)![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 做直線
做直線![]() 軸,在
軸,在![]() 軸上方直線
軸上方直線![]() 上取一點(diǎn)
上取一點(diǎn)![]() ,連接
,連接![]() ,使
,使![]() ,連接
,連接![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,當(dāng)
,當(dāng)![]() 時(shí),求線段
時(shí),求線段![]() 的長(zhǎng);
的長(zhǎng);
(3)在(2)的條件下,點(diǎn)![]() 為第二象限拋物線上的一點(diǎn),連接
為第二象限拋物線上的一點(diǎn),連接![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 做
做![]() 于點(diǎn)
于點(diǎn)![]() ,連接
,連接![]() ,線段
,線段![]() 、
、![]() 分別交線段
分別交線段![]() 于點(diǎn)
于點(diǎn)![]() 、
、![]() ,當(dāng)
,當(dāng)![]() 時(shí),求
時(shí),求![]() 的長(zhǎng)度.
的長(zhǎng)度.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
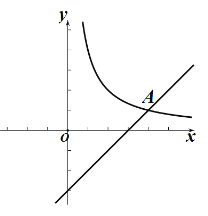
【題目】如圖,在平面直角坐標(biāo)系xOy中,函數(shù)![]() (k>0)的圖象與直線y=x-3相交與點(diǎn)A(4,m).
(k>0)的圖象與直線y=x-3相交與點(diǎn)A(4,m).
(1)求k、m的值;
(2)已知點(diǎn)P(a,a)(a>0),過(guò)點(diǎn)P作垂直于y軸的直線,交直線y=x-3于點(diǎn)M,過(guò)點(diǎn)P作垂直于x軸的直線,交函數(shù)![]() (k>0)的圖象于點(diǎn)N.
(k>0)的圖象于點(diǎn)N.
①當(dāng)a=1時(shí),判斷PM與PN之間的數(shù)量關(guān)系,并說(shuō)明理由;
②若PM≥PN,請(qǐng)結(jié)合函數(shù)圖象,直接寫(xiě)出a的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() .點(diǎn)
.點(diǎn)![]() 為射線
為射線![]() 上一個(gè)動(dòng)點(diǎn),連接
上一個(gè)動(dòng)點(diǎn),連接![]() ,點(diǎn)
,點(diǎn)![]() 在直線
在直線![]() 上,且
上,且![]() .過(guò)點(diǎn)
.過(guò)點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() ,
,![]() 在直線
在直線![]() 的同側(cè),且
的同側(cè),且![]() ,連接
,連接![]() .請(qǐng)用等式表示線段
.請(qǐng)用等式表示線段![]() ,
,![]() ,
,![]() 之間的數(shù)量關(guān)系.小明根據(jù)學(xué)習(xí)函數(shù)的經(jīng)驗(yàn).對(duì)線段
之間的數(shù)量關(guān)系.小明根據(jù)學(xué)習(xí)函數(shù)的經(jīng)驗(yàn).對(duì)線段![]() ,
,![]() ,
,![]() 的長(zhǎng)度之間的關(guān)系進(jìn)行了探究.下面是小明的探究過(guò)程,請(qǐng)補(bǔ)充完整:
的長(zhǎng)度之間的關(guān)系進(jìn)行了探究.下面是小明的探究過(guò)程,請(qǐng)補(bǔ)充完整:
(1)對(duì)于點(diǎn)![]() 在射線
在射線![]() 上的不同位置,畫(huà)圖、測(cè)量,得到了線段
上的不同位置,畫(huà)圖、測(cè)量,得到了線段![]() ,
,![]() ,
,![]() 的長(zhǎng)度的幾組值,如下表:
的長(zhǎng)度的幾組值,如下表:
位置 1 | 位置 2 | 位置 3 | 位置 4 | 位置 5 | 位置 6 | 位置 7 | 位置 8 | |
| 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 |
| 2.10 | 1.32 | 0.53 | 0.00 | 1.32 | 2.10 | 4.37 | 5.6 |
| 0.52 | 1.07 | 1.63 | 2.00 | 2.92 | 3.48 | 5.09 | 5.97 |
在![]() ,
,![]() ,
,![]() 的長(zhǎng)度這三個(gè)量中,確定 的長(zhǎng)度是自變量, 的長(zhǎng)度是這個(gè)自變量的函數(shù), 的長(zhǎng)度是常量.
的長(zhǎng)度這三個(gè)量中,確定 的長(zhǎng)度是自變量, 的長(zhǎng)度是這個(gè)自變量的函數(shù), 的長(zhǎng)度是常量.
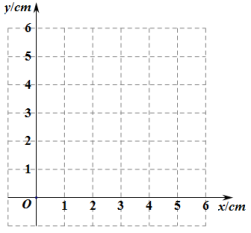
(2)在同一平面直角坐標(biāo)系![]() 中,畫(huà)出(1)中所確定的函數(shù)的圖象;
中,畫(huà)出(1)中所確定的函數(shù)的圖象;
(3)結(jié)合函數(shù)圖象,解決問(wèn)題:請(qǐng)用等式表示線段![]() ,
,![]() ,
,![]() 之間的數(shù)量關(guān)系.
之間的數(shù)量關(guān)系.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com