
【題目】填空,完成下列說理過程
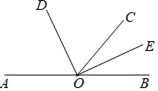
如圖,點A,O,B在同一條直線上,OD,OE分別平分∠AOC和∠BOC.求∠DOE的度數.
解:因為OD是∠AOC的平分線,
所以∠COD=![]() ∠AOC.
∠AOC.
因為OE是∠BOC 的平分線,
所以 =![]() ∠BOC.
∠BOC.
所以∠DOE=∠COD+∠COE=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB= °.
∠AOB= °.
 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖1,直線![]() 分別與y軸、x軸交于點A、點B,點C的坐標為(-3,0),D為直線AB上一動點,連接CD交y軸于點E.
分別與y軸、x軸交于點A、點B,點C的坐標為(-3,0),D為直線AB上一動點,連接CD交y軸于點E.
(1) 點B的坐標為__________,不等式![]() 的解集為___________
的解集為___________
(2) 若S△COE=S△ADE,求點D的坐標;
(3) 如圖2,以CD為邊作菱形CDFG,且∠CDF=60°.當點D運動時,點G在一條定直線上運動,請求出這條定直線的解析式.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題滿分12分)如圖,直線l1的解析表達式為:![]() ,且l1與x軸
,且l1與x軸
交于點D,直線l2經過點A,B,直線l1,l2交于點C.
【1】(1)求直線l2的函數關系式;
【2】(2)求△ADC的面積;
【3】(3)若點H為坐標平面內任意一點,在坐標平面內是否存在這樣的點H,使以A、D、C、H為頂點的四邊形是平行四邊形?若存在,請直接寫出點H的坐標;若不存在,請說明理由.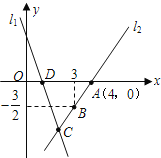
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P,點Q分別代表兩個村莊,直線l代表兩個村莊中間的一條公路.根據居民出行的需要,計劃在公路l上的某處設置一個公交站.
(1)若考慮到村莊P居住的老年人較多,計劃建一個離村莊P最近的車站,請在公路l上畫出車站的位置(用點M表示),依據是 ;
(2)若考慮到修路的費用問題,希望車站的位置到村莊P和村莊Q的距離之和最小,請在公路l上畫出車站的位置(用點N表示),依據是 .
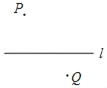
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解放橋是天津市的標志性建筑之一,是一座全鋼結構的部分可開啟的橋梁. (Ⅰ)如圖①,已知解放橋可開啟部分的橋面的跨度AB等于47m,從AB的中點C處開啟,則AC開啟至AC′的位置時,AC′的長為 ![]() m;
m;
(Ⅱ)如圖②,某校數學興趣小組要測量解放橋的全長PQ,在觀景平臺M處測得∠PMQ=54°,沿河岸MQ前行,在觀景平臺N處測得∠PNQ=73°,已知PQ⊥MQ,MN=40m,求解放橋的全長PQ(tan54°≈1.4,tan73°≈3.3,結果保留整數).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,點E、F分別為AB、CD上的點,且AE=CF= ![]() AB,點O為線段EF的中點,過點O作直線與正方形的一組對邊分別交于P、Q兩點,并且滿足PQ=EF,則這樣的直線PQ(不同于EF)有條.
AB,點O為線段EF的中點,過點O作直線與正方形的一組對邊分別交于P、Q兩點,并且滿足PQ=EF,則這樣的直線PQ(不同于EF)有條. 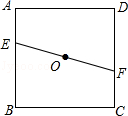
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】
![]()
(1)填空:點B在數軸上表示的數是 ,點C在數軸上表示的數是 ;
(2)若線段CD以每秒3個單位的速度向右勻速運動,當點D運動到A時,線段CD與線段AB開始有重疊部分,此時線段CD運動了 秒;
(3)在(2)的條件下,線段CD繼續向右運動,問再經過 秒后,線段CD與線段AB不再有重疊部分;
(4)若線段AB、CD同時從圖中位置出發,線段AB以每秒2個單位的速度向左勻速運動,線段CD仍以每秒3個單位的速度向右勻速運動,點P是線段CD的中點,問運動幾秒時,點P與線段AB兩端點(A或B)的距離為1個單位?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com