
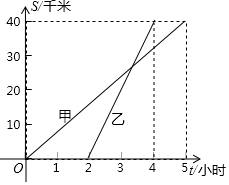
 甲、乙兩人沿相同的路線由A地到B地勻速前進,已知A,B兩地間的距離為40千米,它們前進的路程記為s(單位:千米),甲出發后的時間記為t(單位:小時),甲、乙前進的路程與時間的函數圖象如圖所示,根據圖象信息回答下列問題:
甲、乙兩人沿相同的路線由A地到B地勻速前進,已知A,B兩地間的距離為40千米,它們前進的路程記為s(單位:千米),甲出發后的時間記為t(單位:小時),甲、乙前進的路程與時間的函數圖象如圖所示,根據圖象信息回答下列問題:分析 (1)根據速度、路程、時間之間的關系即可解決問題.
(2)利用待定系數法即可解決.
(3)利用方程組求出兩個函數圖象的交點的橫坐標,即可求得相遇時間
解答 解:(1)甲的速度是$\frac{40}{5}$=8千米/小時,乙比甲晚出發2小時,
故答案為8,2.
(2)設S甲的解析式為s=kt,則有5k=40,k=8,
∴S=8t,
S乙與的解析式為y=mx+n,則有$\left\{\begin{array}{l}{2m+n=0}\\{4m+n=40}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=20}\\{n=-40}\end{array}\right.$,
∴s=20t-40.
(3)由$\left\{\begin{array}{l}{s=8t}\\{s=20t-40}\end{array}\right.$,解得t=$\frac{10}{3}$,
40-$\frac{80}{3}$=$\frac{40}{3}$,
∴乙經過$\frac{10}{3}$小時可以追上甲,此時兩人距離B地還有$\frac{40}{3}$千米.
點評 本題考查的是一次函數的應用問題,解題關鍵是要讀懂題目的意思,根據題目給出的條件,找出合適的等量關系,列出函數式,再求解.


 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案科目:初中數學 來源: 題型:解答題
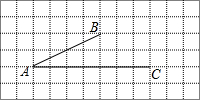 在如圖所示的網格中,每個小正方形的邊長為1,每個小正方形的頂點都叫做格點,已知線段AB、AC的端點都在格點上.
在如圖所示的網格中,每個小正方形的邊長為1,每個小正方形的頂點都叫做格點,已知線段AB、AC的端點都在格點上.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,△ABC的頂點坐標分別為A(4,4),B(2,1),C(5,1).
如圖,△ABC的頂點坐標分別為A(4,4),B(2,1),C(5,1).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com