
如圖,在Rt△ABC中,∠C=90°,O是斜邊AB上的中點(diǎn),AE=CE,BF∥AC.
(1)求證:△AOE≌△BOF;
(2)求證:四邊形BCEF是矩形.


【考點(diǎn)】全等三角形的判定與性質(zhì);矩形的判定.
【專題】證明題.
【分析】(1)根據(jù)平行線性質(zhì)得出∠A=∠OBF,根據(jù)ASA推出兩三角形全等即可.
(2)根據(jù)全等得出AE=BF=CE,推出四邊形是平行四邊形,根據(jù)矩形的判定推出即可.
【解答】證明:(1)∵BF∥AC,
∴∠A=∠OBF,
在△AOE和△BOF中,
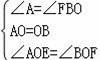
 ,
,
∴△AOE≌△BOF(ASA).
(2)∵△AOE≌△BOF,
∴AE=BF,
∵AE=CE,
∴CE=BF,
又∵CE∥BF,
∴四邊形BCEF是平行四邊形,
又∵∠C=90°
∴四邊形BCEF是矩形.
【點(diǎn)評(píng)】本題考查了平行線的性質(zhì),全等三角形的性質(zhì)和判定,矩形的判定,平行四邊形的判定的應(yīng)用,題目比較好,主要考查學(xué)生的推理能力.


 全能測(cè)控一本好卷系列答案
全能測(cè)控一本好卷系列答案 發(fā)散思維新課堂系列答案
發(fā)散思維新課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
如圖,數(shù)軸上A,B兩點(diǎn)表示的數(shù)分別為﹣1和
 ,點(diǎn)B關(guān)于點(diǎn)A的對(duì)稱點(diǎn)為C,則點(diǎn)C所表示的數(shù)為( )
,點(diǎn)B關(guān)于點(diǎn)A的對(duì)稱點(diǎn)為C,則點(diǎn)C所表示的數(shù)為( )

A.﹣2﹣
 B.﹣1﹣
B.﹣1﹣
 C.﹣2+
C.﹣2+
 D.1+
D.1+

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
在矩形ABCD中,AD=5,AB=3,AE平分∠BAD交BC邊于點(diǎn)E,則線段BE,EC的長(zhǎng)度分別為( )


A.2和3 B.3和2 C.4和1 D.1和4
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
遵義市某中學(xué)為了搞好“創(chuàng)建全國(guó)文明城市”的宣傳活動(dòng),對(duì)本校部分學(xué)生(隨機(jī)抽查)進(jìn)行了一次相關(guān)知識(shí)了解程度的調(diào)查測(cè)試(成績(jī)分為A、B、C、D、E五個(gè)組,x表示測(cè)試成績(jī)).通過對(duì)測(cè)試成績(jī)的分析,得到如圖所示的兩幅不完整的統(tǒng)計(jì)圖.請(qǐng)你根據(jù)圖中提供的信息解答以下問題:


(1)參加調(diào)查測(cè)試的學(xué)生為 人;
(2)將條形統(tǒng)計(jì)圖補(bǔ)充完整;
(3)本次調(diào)查測(cè)試成績(jī)中的中位數(shù)落在 組內(nèi);
(4)若測(cè)試成績(jī)?cè)?0分以上(含80分)為優(yōu)秀,該中學(xué)共有學(xué)生2600人,請(qǐng)你根據(jù)樣本數(shù)據(jù)估計(jì)全校學(xué)生測(cè)試成績(jī)?yōu)閮?yōu)秀的總?cè)藬?shù).
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com