
如圖,在矩形ABCD中,AB=6cm,AD=8cm,點P從點A出發沿AD向點D勻速運動,速度是1cm/s,過點P作PE∥AC交DC于點E.同時,點Q從點C出發沿CB方向,在射線CB上勻速運動,速度是2cm/s,連接PQ,QE,PQ與AC交與點F,設運動時間為t(s)(0<t<8).
(1)當t為何值時,四邊形PFCE是平行四邊形;
(2)設△PQE的面積為s(cm2),求s與t之間的函數關系式;
(3)是否存在某一時刻t,使得△PQE的面積為矩形ABCD面積的
 ;
;
(4)是否存在某一時刻t,使得點E在線段PQ的垂直平分線上.


解:(1)PD=8﹣t,CQ=2t,根據題意得:8﹣t=2t,解得:t=
 ;
;
(2)S四邊形PDCQ=
 (PD+CQ)•CD=
(PD+CQ)•CD=
 ×6(8﹣t+2t)=3(8+t)=3t+24,
×6(8﹣t+2t)=3(8+t)=3t+24,
∵PE∥AC,∴
 ,∴
,∴
 =
=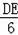
 ,則DE=﹣
,則DE=﹣
 t+6,則EC=6﹣(﹣
t+6,則EC=6﹣(﹣
 t+6)=
t+6)=
 t,
t,
則S△PDE=
 PD•DE=
PD•DE=
 (8﹣t)•(﹣
(8﹣t)•(﹣
 t+6),S△CQE=
t+6),S△CQE=
 CQ•EC=
CQ•EC=
 ×2t•
×2t•
 t=
t=
 t2,
t2,
則s=3t+24﹣
 (8﹣t)•(﹣
(8﹣t)•(﹣
 t+6)﹣
t+6)﹣
 t2,即s=﹣
t2,即s=﹣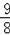
 t2+3t;
t2+3t;
(3)S矩形ABCD=6×8=48,根據由題意得:﹣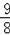
 t2+3t=
t2+3t=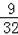
 ×48,解得:t=2或6;
×48,解得:t=2或6;
(4)在直角△PDE中,PD2=(8﹣t)2+(﹣
 t+6)2,
t+6)2,
在直角△COQ中,QE2=(2t)2+(
 t)2,
t)2,
當點E在線段PQ的垂直平分線上時,PD2=QE2,
則(8﹣t)2+(﹣
 t+6)2=(2t)2+(
t+6)2=(2t)2+(
 t)2,
t)2,
解得:t=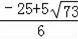
 或
或
 (舍去).則t=
(舍去).則t=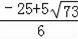
 .
.


 周周清檢測系列答案
周周清檢測系列答案 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案科目:初中數學 來源: 題型:
已知△ABC 中, ,
, ,D為BC邊延長線上一點,BM平分
,D為BC邊延長線上一點,BM平分 ,E
,E 為射線BM上一點.
為射線BM上一點.
(1)如圖1,連接CE,
①若CE∥AB,求 的度數;
的度數;
②若CE平分 ,求
,求 的度數.
的度數.
 (2)若直線CE垂直于△ABC的一邊,請直接寫出∠BEC的度數.
(2)若直線CE垂直于△ABC的一邊,請直接寫出∠BEC的度數.

25題圖1 25題備用圖
查看答案和解析>>
科目:初中數學 來源: 題型:
二次函數y=ax2+bx+c(a,b,c為常數,且a≠0)中的x與y的部分對應值如下表:

①ac<0;②當x>1時,y的值隨x值的增大而減小;③x=2是方程ax2+(b﹣1)x+c=0的一個根;
④當﹣1<x<2時,ax2+(b﹣1)x+c>0.上述結論中正確的有 個.( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com