
【題目】如圖1,在一張長方形紙條上畫一條數軸.
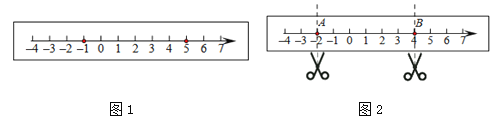
(1)折疊紙條使數軸上表示![]() 的點與表示5的點重合,折痕與數軸的交點表示的數是 ;
的點與表示5的點重合,折痕與數軸的交點表示的數是 ;
(2)如果數軸上兩點之間的距離為8,經過(1)的折疊方式能夠重合,那么左邊這個點表示的數是 ;
(3)如圖2,點A、B表示的數分別是![]() 、
、![]() ,數軸上有點C,使得AC=2BC,那么點C表示的數是 ;
,數軸上有點C,使得AC=2BC,那么點C表示的數是 ;
(4)如圖2,若將此紙條沿A、B兩處剪開,將中間的一段紙條對折,使其左右兩端重合,這樣連續對折![]() 次后,再將其展開,求最左端的折痕與數軸的交點表示的數.(用含
次后,再將其展開,求最左端的折痕與數軸的交點表示的數.(用含![]() 的代數式表示)
的代數式表示)
【答案】(1)2;(2)![]() ; (3)2或10;(4)
; (3)2或10;(4)![]() .
.
【解析】
(1)找出5表示的點與﹣1表示的點組成線段的中點表示數,然后結合數軸即可求得答案;
(2)由2平分兩個點組成的線段,得到左邊的點為2-距離的一半,從而可求得答案;
(3)設點C表示的數為x,分三種情況討論:①點C在A的左側,②點C在A和B之間,③點C在B的右側.
(4)先求出每兩條相鄰折痕的距離,進一步得到最左端的折痕和最右端的折痕與數軸的交點表示的數,即可求得答案.
(1)(﹣1+5)÷2=4÷2=2.
故折痕與數軸的交點表示的數為2;
(2)2-8÷2=2-4=-2;
(3)設點C表示的數為x,分三種情況討論:
①點C在A的左側,此時AC<BC,與AC=2BC矛盾,此種情況不成立;
②點C在A和B之間,此時:x+2=2(4-x),解得:x=2;
③點C在B的右側,此時:x+2=2(x-4),解得:x=10.
綜上所述:點C表示的數是2或10.
(4)∵對折n次后,每兩條相鄰折痕的距離為![]() =
=![]() ,∴最左端的折痕與數軸的交點表示的數是﹣2+
,∴最左端的折痕與數軸的交點表示的數是﹣2+![]() .
.


 步步高達標卷系列答案
步步高達標卷系列答案科目:初中數學 來源: 題型:
【題目】圖1是某城市四月份1至8日的日最高氣溫隨時間變化的折線統計圖,小剛根據圖1將數據統計整理后制成了圖2.
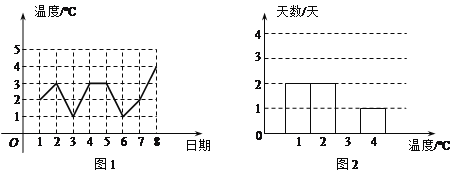
根據圖中信息,解答下列問題:
(1)將圖2補充完整;
(2)這8天的日最高氣溫的中位數是 C;
(3)計算這8天的日最高氣溫的平均數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】谷歌人工智能AlphaGo機器人與李世石的圍棋挑戰賽引起人們的廣泛關注,人工智能完勝李世石.某教學網站開設了有關人工智能的課程并策劃了A,B兩種網上學習的月收費方式:
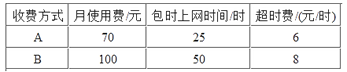
設小明每月上網學習人工智能課程的時間為x小時,方案A,B的收費金額分別為yA元、yB元.
(1)當x≥50時,分別求出yA、yB與x之間的函數表達式;
(2)若小明3月份上該網站學習的時間為60小時,則他選擇哪種方式上網學習合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列從左到右的變形,是因式分解的是( )
A. m2-1=(m+1)(m-1) B. 2(a-b)=2a-2b C. x2-2x+1=x(x-2)+1, D. a(a-b)(b+1)=(a2 -ab)(b+1)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+c(a<0,c>0)與x軸交于A,B兩點,與y軸交于點C,其對稱軸l為x=﹣1,直線y=kx+m經過A,C兩點,與拋物線的對稱軸l交于點D,且AD=2CD,連接BC,BD.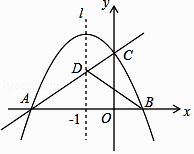
(1)求A,B兩點的坐標;
(2)求證:a=﹣k;
(3)若△BCD是直角三角形,求拋物線的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:正方形紙片ABCD的邊長為4,將該正方形紙片沿EF折疊(E,F分別在AB,CD邊上),使點B落在AD邊上的點M處,點C落在點N處,MN與CD交于點P.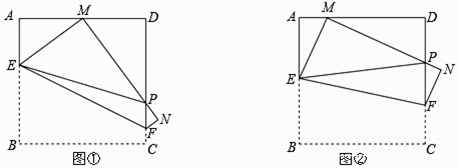
(1)如圖①,連接PE,若M是AD邊的中點.
①寫出圖中與△PMD相似的三角形.
②求△PMD的周長.
(2)如圖②,隨著落點M在AD邊上移動(點M不與A、D重合),△PDM的周長是否發生變化?請說明你的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,∠C=120°,AD=2AB=4,點H、G分別是邊CD、BC上的動點.連接AH、HG,點E為AH的中點,點F為GH的中點,連接EF.則EF的最大值與最小值的差為( )

A. 1 B. ![]() ﹣1 C.
﹣1 C. ![]() D. 2﹣
D. 2﹣![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】以四邊形ABCD的邊AB、AD為邊分別向外側作等邊三角形ABF和ADE,連接EB、FD,交點為G.
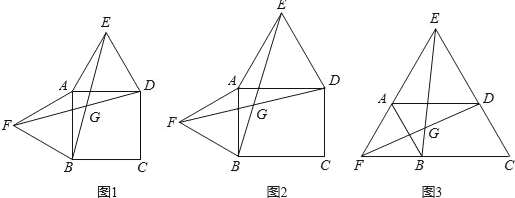
(1)當四邊形ABCD為正方形時(如圖1),EB和FD的數量關系是 ;
(2)當四邊形ABCD為矩形時(如圖2),EB和FD具有怎樣的數量關系?請加以證明;
(3)四邊形ABCD由正方形到矩形到一般平行四邊形的變化過程中,∠EGD是否發生變化?如果改變,請說明理由;如果不變,請在圖3中求出∠EGD的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com