
【題目】如圖,已知拋物線y=ax2+bx+c(a<0,c>0)與x軸交于A,B兩點,與y軸交于點C,其對稱軸l為x=﹣1,直線y=kx+m經過A,C兩點,與拋物線的對稱軸l交于點D,且AD=2CD,連接BC,BD.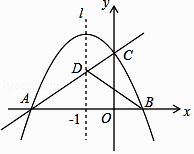
(1)求A,B兩點的坐標;
(2)求證:a=﹣k;
(3)若△BCD是直角三角形,求拋物線的解析式.
【答案】
(1)
解:如圖,設對稱軸l與x軸的交點為E,
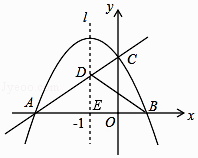
∵l∥y軸,
∴ ![]() =
= ![]() ,且AD=2DC,
,且AD=2DC,
∴AE=2EO,
∵對稱軸l為x=1,
∴E(﹣1,0),則EO=1,
∴AE=2,則OA=3,
∴A(﹣3,0),
∵A、B關于對稱軸l對稱,
∴BE=AE=2,則OB=1,
∴B(1,0)
(2)
證明:∵拋物線經過A(﹣3,0)和B(1,0),
∴拋物線解析式為y=a(x+3)(x﹣1),即y=ax2+2ax﹣3a,
∵拋物線與y軸交于點C,
∴C(0,﹣3a),
∵直線y=kx+m經過A、C兩點,
∴ ![]() ,解得m=3k,
,解得m=3k,
∴C(0,3k),
∴﹣3a=3k,即a=﹣k
(3)
解:由(1)、(2)可知B(1,0),C(0,3k),D(﹣1,2k),
∴BC2=1+9k2,BD2=4+4k2,CD2=1+k2,
∵在Rt△BCO中,∠CBD<∠CBO<90°,
∴∠CBD為銳角,
∴只可能當∠BCD或∠BDC為直角時,△BCD才是直角三角形,
①當∠BCD為直角時,則有BC2+CD2=BD2,
∴1+9k2+1+k2=4+4k2,即k2= ![]() ,
,
∵k>0,
∴k= ![]() ,
,
∴a=﹣k=﹣ ![]() ,
,
∴拋物線解析式為y=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() ;
;
②當∠BDC為直角時,則有BD2+CD2=BC2,
∴4+4k2+1+k2=1+9k2,即k2=1,
∵k>0,
∴k=1,
∴a=﹣k=﹣1,
∴拋物線解析式為y=﹣x2﹣2x+3;
綜上可知拋物線解析式為y=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() 或y=﹣x2﹣2x+3
或y=﹣x2﹣2x+3
【解析】(1)設對稱軸x與x軸交點為E,由平行線分線段成比例可求得AE的長,則可求得A點坐標,再利用拋物線的對稱性可求得B點坐標;(2)把A、B兩點的坐標代入拋物線解析式,可用a表示出C點的坐標,再由直線AC的解析式可用k表示出C點坐標,則可得到a和k的關系;(3)用k可表示出C、D的坐標,利用勾股定理可表示出BC2、BD2和CD2 , 分∠BDC=90°和∠BCD=90°兩種情況可分別求得k的值,可求得k的值,可求得a的值,則可求出拋物線的解析式.


科目:初中數學 來源: 題型:
【題目】任何實數a,可用[a]表示不超過a的最大整數,如[4]=4,[![]() ]=1.現對72進行如下操作:72
]=1.現對72進行如下操作:72![]() [
[![]() ]=8
]=8![]() [
[![]() ]=2
]=2![]() [
[![]() ]=1,這樣對72進行3次操作后變為1,類似地,①對81進行________次操作后變為1;②進行3次操作后變為1的所有正整數中,最大的是________.
]=1,這樣對72進行3次操作后變為1,類似地,①對81進行________次操作后變為1;②進行3次操作后變為1的所有正整數中,最大的是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
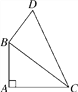
【題目】如圖所示,在四邊形ABDC中,∠A=90°,AB=9,AC=12,BD=8,CD=17.
(1)連接BC,求BC的長;
(2)求四邊形ABDC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在一張長方形紙條上畫一條數軸.
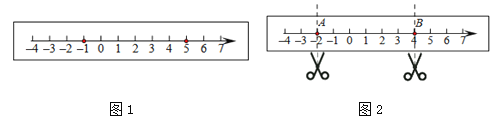
(1)折疊紙條使數軸上表示![]() 的點與表示5的點重合,折痕與數軸的交點表示的數是 ;
的點與表示5的點重合,折痕與數軸的交點表示的數是 ;
(2)如果數軸上兩點之間的距離為8,經過(1)的折疊方式能夠重合,那么左邊這個點表示的數是 ;
(3)如圖2,點A、B表示的數分別是![]() 、
、![]() ,數軸上有點C,使得AC=2BC,那么點C表示的數是 ;
,數軸上有點C,使得AC=2BC,那么點C表示的數是 ;
(4)如圖2,若將此紙條沿A、B兩處剪開,將中間的一段紙條對折,使其左右兩端重合,這樣連續對折![]() 次后,再將其展開,求最左端的折痕與數軸的交點表示的數.(用含
次后,再將其展開,求最左端的折痕與數軸的交點表示的數.(用含![]() 的代數式表示)
的代數式表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在學習一元一次不等式與一次函數中,小明在同一個坐標系中分別做出了一次函數l1和l2的圖像,l1與坐標軸的交點分別為點A、點B,l1與l2的交點為點C,但被同桌小英不小心用墨水給部分污染了,我們一起來探討
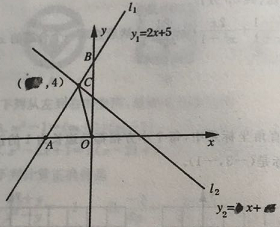
(1)寫出點A、點C的坐標:A(①,0);C(②,4);
(2)求△BOC的面積:S△BOC=③
(3)直接寫出不等式2x+5<·x+·的解集并回答下面問題
在解決問題(3)時,小明和小英各抒己見.小明:“l2的表達式中已經看不清楚了,并且只知道l2上一個點C的坐標,求不出該直線的表達式,所以無法求出該不等式的解集”小英說:“不用求出l2的表達式就可以得出該不等式的解集.”你同意誰的說法?并說明理由
查看答案和解析>>
科目:初中數學 來源: 題型:
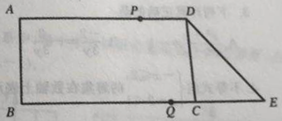
【題目】如圖,在平行四邊形ABCD中,∠B=90°,且AD=9cm,AB=4cm,延長BC到點E,使CE=3cm,連接DE.若動點P從A點出發,以每秒2cm的速度沿線段AD運動;動點Q從E點出發以每秒3cm的速度沿EB向B點運動,當點P、Q有一個到位置時,動點P、Q同時停止運動,設點P、Q同時出發,并運動了t秒,回答下列問題:
(1)求DE的長
(2)當t為多少時,四邊形PQED成為平行四邊形;
(3)請直接寫出使得△DQE是等腰三角形時t的值
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是一次函數y=kx+b的圖象,以下說法中正確的是( )

A. 直線與y軸的交點為(3,0) B. y隨x的增大而增大
C. 直線與兩坐標軸圍成的三角形面積是6 D. 一元一次方程kx+b=0的解為x=2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com