
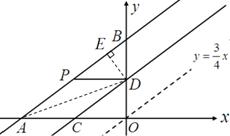
如圖,直線 與
與 軸相交于點
軸相交于點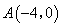 ,與
,與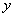 軸相交于點
軸相交于點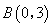 ,點
,點 從點
從點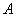 出發(fā),以每秒
出發(fā),以每秒 個單位長度的速度沿直線
個單位長度的速度沿直線 向點
向點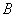 移動。同時,將直線
移動。同時,將直線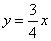 以每秒
以每秒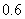 個單位長度的速度向上平移,交
個單位長度的速度向上平移,交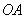 于點
于點 ,交
,交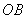 于點
于點 ,設(shè)運動時間為
,設(shè)運動時間為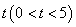 秒。
秒。
⑴證明:在運動過程中,四邊形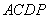 總是平行四邊形;
總是平行四邊形;
⑵當(dāng)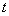 取何值時,四邊形
取何值時,四邊形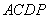 為菱形?請指出此時以點
為菱形?請指出此時以點 為圓心、
為圓心、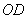 長為半徑的圓與直線
長為半徑的圓與直線 的位置關(guān)系并說明理由。
的位置關(guān)系并說明理由。
解:⑴∵直線 與
與 軸相交于點
軸相交于點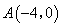 ,與
,與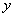 軸相交于點
軸相交于點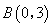
∴直線 的解析式為
的解析式為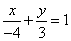 ,即
,即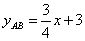
∵將直線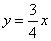 以每秒
以每秒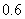 個單位長度的速度向上平移
個單位長度的速度向上平移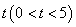 秒得到直線
秒得到直線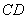
∴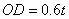 ,∴
,∴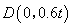 ,∴直線
,∴直線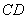 的解析式為
的解析式為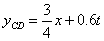
∵在直線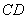 中,點
中,點 在
在 軸上,∴令
軸上,∴令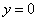 ,則
,則 ,∴
,∴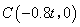 ,
,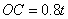
∴在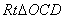 中,
中,
∵點 從點
從點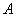 出發(fā),以每秒
出發(fā),以每秒 個單位長度的速度沿直線
個單位長度的速度沿直線 向點
向點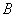 移動
移動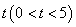 秒
秒
∴ ,∴
,∴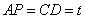 ,又∵
,又∵ ,∴
,∴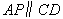 ,
,
∵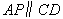 ,
,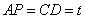 ,∴在運動過程中,四邊形
,∴在運動過程中,四邊形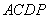 總是平行四邊形;
總是平行四邊形;
⑵欲使四邊形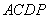 為菱形,只需在
為菱形,只需在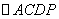 中滿足條件
中滿足條件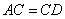 ,即
,即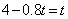 ,解得
,解得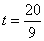
∴當(dāng)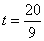 時,四邊形
時,四邊形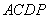 為菱形;
為菱形;
此時以點 為圓心、
為圓心、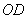 長為半徑的圓與直線
長為半徑的圓與直線 相切,理由如下:
相切,理由如下:
∵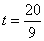 ,∴
,∴ ,∴
,∴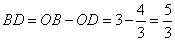
∵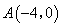 ,
,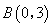 ,∴
,∴ ,
,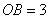 ,∴在
,∴在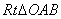 中,
中,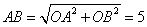
過點 作
作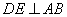 于點
于點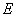 ,則
,則
∵在 和
和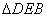 中,
中,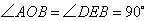 且
且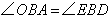 ,∴
,∴ ∽
∽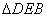
∴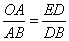 ,即
,即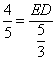 ,∴
,∴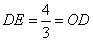 ,∴點
,∴點 到直線
到直線 的距離等于
的距離等于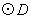 的半徑
的半徑
∴以點 為圓心、
為圓心、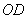 長為半徑的圓與直線
長為半徑的圓與直線 相切。
相切。
另解:(在證明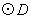 與直線
與直線 相切時,也可利用等積法求得點
相切時,也可利用等積法求得點 到直線
到直線 的距離。)
的距離。)
設(shè)點 到直線
到直線 的距離為
的距離為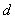 ,則
,則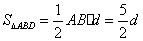 ,連結(jié)
,連結(jié)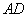 ,
,
∵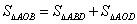 且
且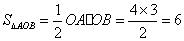 、
、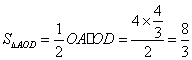
∴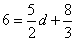 ,解得
,解得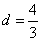 ,∴點
,∴點 到直線
到直線 的距離與
的距離與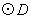 的半徑相等,即
的半徑相等,即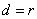
∴以點 為圓心、
為圓心、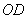 長為半徑的
長為半徑的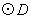 與直線
與直線 相切。
相切。
再解:(巧用“菱形對角線的性質(zhì)”和“角平分線性質(zhì)定理”)
連結(jié)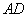 ,則
,則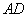 是菱形
是菱形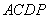 的對角線,∴
的對角線,∴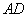 平分
平分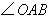
∵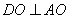 ,∴
,∴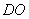 是點
是點 到直線
到直線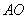 的距離,
的距離,
∴點 到直線
到直線 的距離=點
的距離=點 到直線
到直線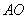 的距離
的距離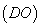
∴以點 為圓心、
為圓心、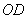 長為半徑的圓與直線
長為半徑的圓與直線 相切。
相切。


科目:初中數(shù)學(xué) 來源: 題型:
閱讀理解:如圖3,在平面內(nèi)選一定點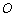 ,引一條有方向的射線
,引一條有方向的射線 ,再選定一個單位長度,那么平面上任一點M的位置可由
,再選定一個單位長度,那么平面上任一點M的位置可由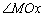 的度數(shù)
的度數(shù)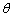 與
與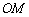 的長度m確定,有序數(shù)對(
的長度m確定,有序數(shù)對(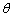 ,m)稱為
,m)稱為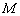 點的“極坐標(biāo)”,這樣建立的坐標(biāo)系稱為“極坐標(biāo)系”.
點的“極坐標(biāo)”,這樣建立的坐標(biāo)系稱為“極坐標(biāo)系”.
應(yīng)用:在圖4的極坐標(biāo)系下,如果正六邊形的邊長為2,有一邊OA在射線 上,則正六邊形的頂點C的極坐標(biāo)應(yīng)記為
上,則正六邊形的頂點C的極坐標(biāo)應(yīng)記為
A.(60°,4) B.(45°,4) C.(60°,2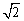 ) D.(50°,2
) D.(50°,2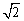 )
)
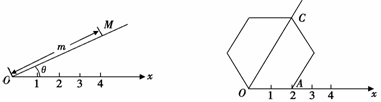
圖3  圖4
圖4
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
在“黃袍山國家油茶產(chǎn)業(yè)示范園”建設(shè)中,某農(nóng)戶計劃購買甲、乙兩種油茶樹苗共1000株.已知乙種樹苗比甲種樹苗每株貴3元,且用100元錢購買甲種樹苗的株數(shù)與用160元錢購買乙種樹苗的株數(shù)剛好相同.
(1)求甲、乙兩種油茶樹苗每株的價格;
(2)如果購買兩種樹苗共用5600元,那么甲、乙兩種樹苗各買了多少株?
(3)調(diào)查統(tǒng)計得,甲、乙兩種樹苗的成活率分別為90%,95%.要使這批樹苗的成活率不低于92%,且使購買樹苗的費用最低,應(yīng)如何選購樹苗?最低費用是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
為了了解我市的空氣質(zhì)量情況,某環(huán)保興趣小組從環(huán)境監(jiān)測網(wǎng)隨機(jī)抽取了我市若干天的空氣質(zhì)量情況作為樣本進(jìn)行統(tǒng)計,繪制了如圖所示的條形統(tǒng)計圖和扇形統(tǒng)計圖(部分信息未給出)。
我市若干天空氣質(zhì)量情況條形統(tǒng)計圖 我市若干天空氣質(zhì)量情況扇形統(tǒng)計圖
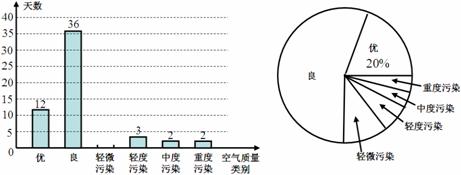
請你根據(jù)圖中提供的信息,解答下列問題:
⑴請補(bǔ)全條形統(tǒng)計圖;
⑵求扇形統(tǒng)計圖中表示“優(yōu)”的扇形的圓心角度數(shù);
⑶請估計我市這一年(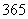 天)達(dá)到“優(yōu)”和“良”的總天數(shù)。
天)達(dá)到“優(yōu)”和“良”的總天數(shù)。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
如果將拋物線y=x2向右平移1個單位,那么所得的拋物線的表達(dá)式是().
(A) y=x2-1; (B) y=x2+1; (C) y=(x-1)2; (D) y=(x+1)2.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com