
如圖,點A(3,5)關于原點O的對稱點為點C,分別過點A,C作y軸的平行線,與反比例函數y=
 (0<k<15)的圖象交于點B,D,連接AD,BC,AD與x軸交于點E(﹣2,0).
(0<k<15)的圖象交于點B,D,連接AD,BC,AD與x軸交于點E(﹣2,0).
(1)求k的值;
(2)直接寫出陰影部分面積之和.
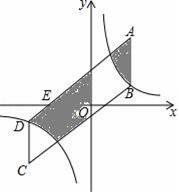

【考點】反比例函數與一次函數的交點問題.
【分析】(1)根據點A和點E的坐標求得直線AE的解析式,然后設出點D的縱坐標,代入直線AE的解析式即可求得點D的坐標,從而求得k值;
(2)根據中心對稱的性質得到陰影部分的面積等于平行四邊形CDGF的面積即可.
【解答】解:(1)∵A(3,5)、E(﹣2,0),
∴設直線AE的解析式為y=kx+b,
則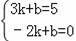
 ,
,
解得: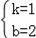
 ,
,
∴直線AE的解析式為y=x+2,
∵點A(3,5)關于原點O的對稱點為點C,
∴點C的坐標為(﹣3,﹣5),
∵CD∥y軸,
∴設點D的坐標為(﹣3,a),
∴a=﹣3+2=﹣1,
∴點D的坐標為(﹣3,﹣1),
∵反比例函數y=
 (0<k<15)的圖象經過點D,
(0<k<15)的圖象經過點D,
∴k=﹣3×(﹣1)=3;
(2)如圖:
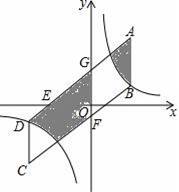

∵點A和點C關于原點對稱,
∴陰影部分的面積等于平行四邊形CDGF的面積,
∴S陰影=4×3=12.
【點評】本題考查了反比例函數與一次函數的交點問題,解題的關鍵是能夠確定點D的坐標,難度不大.


 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案 天天練口算系列答案
天天練口算系列答案科目:初中數學 來源: 題型:
如圖,P是Rt△ABC的斜邊BC上異于B、C的一點,過P點作直線截△ABC,使截得的三角形與△ABC相似,滿足這樣條件的直線共有( )
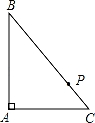
A.1條 B.2條 C.3條 D.4條
查看答案和解析>>
科目:初中數學 來源: 題型:
在平面直角坐標系xOy中,點A關于原點的對稱點的坐標為(﹣2,1),則點A坐標為( )
A.(﹣2,﹣1) B.(2,﹣1) C.(2,1) D.(﹣l,2)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com