
如圖,AB是⊙O的直徑,
 =
=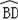
 ,連接ED、BD,延長AE交BD的延長線于點M,過點D作⊙O的切線交AB的延長線于點C.
,連接ED、BD,延長AE交BD的延長線于點M,過點D作⊙O的切線交AB的延長線于點C.
(1)若OA=CD=2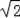
 ,求陰影部分的面積;
,求陰影部分的面積;
(2)求證:DE=DM.
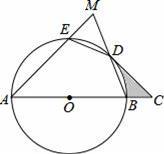

【考點】切線的性質;扇形面積的計算.
【專題】證明題.
【分析】(1)連接OD,根據已知和切線的性質證明△OCD為等腰直角三角形,得到∠DOC=45°,根據S陰影=S△OCD﹣S扇OBD計算即可;
(2)連接AD,根據弦、弧之間的關系證明DB=DE,證明△AMD≌△ABD,得到DM=BD,得到答案.
【解答】(1)解:如圖,連接OD,
∵CD是⊙O切線,
∴OD⊥CD,
∵OA=CD=2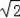
 ,OA=OD,
,OA=OD,
∴OD=CD=2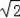
 ,
,
∴△OCD為等腰直角三角形,
∴∠DOC=∠C=45°,
∴S陰影=S△OCD﹣S扇OBD=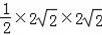
 ﹣
﹣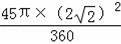
 =4﹣π;
=4﹣π;
(2)證明:如圖,連接AD,
∵AB是⊙O直徑,
∴∠ADB=∠ADM=90°,
又∵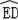
 =
=
 ,
,
∴ED=BD,∠MAD=∠BAD,
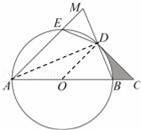
在△AMD和△ABD中,
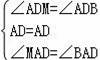
 ,
,
∴△AMD≌△ABD,
∴DM=BD,
∴DE=DM.

【點評】本題考查的是切線的性質、弦、弧之間的關系、扇形面積的計算,掌握切線的性質定理和扇形的面積公式是解題的關鍵,注意輔助線的作法.


科目:初中數學 來源: 題型:
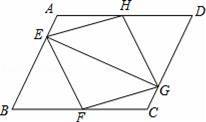
如圖,已知:在平行四邊形ABCD中,點E、F、G、H分別在邊AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.求證:
(1)△AEH≌△CGF;
(2)四邊形EFGH是菱形.

查看答案和解析>>
科目:初中數學 來源: 題型:
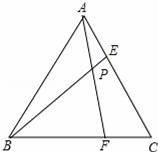
等邊三角形ABC的邊長為6,在AC,BC邊上各取一點E,F,連接AF,BE相交于點P.
(1)若AE=CF;
①求證:AF=BE,并求∠APB的度數;
②若AE=2,試求AP•AF的值;
(2)若AF=BE,當點E從點A運動到點C時,試求點P經過的路徑長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com