
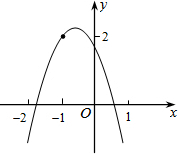
 如圖所示,二次函數 y=ax2+bx+c (a≠0)的圖象經過點(-1,2),且與x軸交點的橫坐標分別為x1,x2,其中-2<x1<-1,0<x2<1,下列結論(1)4a-2b+c<0;(2)2a-b<0;(3)a-3b>0;(4)b2+8a<4ac; 其中正確的有(1),(2),(3).
如圖所示,二次函數 y=ax2+bx+c (a≠0)的圖象經過點(-1,2),且與x軸交點的橫坐標分別為x1,x2,其中-2<x1<-1,0<x2<1,下列結論(1)4a-2b+c<0;(2)2a-b<0;(3)a-3b>0;(4)b2+8a<4ac; 其中正確的有(1),(2),(3). 分析 由拋物線的開口方向判斷a與0的關系,由拋物線與y軸的交點判斷c與0的關系,然后根據對稱軸及拋物線與x軸交點情況進行推理,進而對所得結論進行判斷.
解答 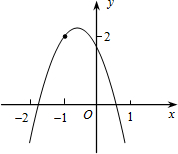 解:(1)根據圖象知,當x=-2時,y<0,即4a-2b+c<0;故本選項正確;
解:(1)根據圖象知,當x=-2時,y<0,即4a-2b+c<0;故本選項正確;
(2)∵該函數圖象的開口向下,∴a<0;
又對稱軸-1<x=-$\frac{b}{2a}$<0,∴2a-b<0,故本選項正確;
(3)∵a<0,-$\frac{b}{2a}$<0,
∴b<0,
∵二次函數y=ax2+bx+c(a≠0)的圖象經過點(-1,2),
∴a-b+c=2,
∵0<c<2,
∴a-b=2-c>0,
則a-3b>0.
故本選項正確;
(4)∵y=$\frac{4ac-{b}^{2}}{4a}$>2,a<0,
∴4ac-b2<8a,即b2+8a>4ac,故本選項錯誤.
綜上所述,正確的結論有3個;
故答案為:(1),(2),(3).
點評 本題主要考查對二次函數圖象與系數的關系,拋物線與x軸的交點,二次函數圖象上點的坐標特征等知識點的理解和掌握.二次函數y=ax2+bx+c系數符號的確定由拋物線開口方向、對稱軸、拋物線與y軸的交點、拋物線與x軸交點的個數確定.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{{{x^2}-1}}{x-1}=\frac{{{{(x-1)}^2}}}{x-1}=\frac{1}{x-1}$ | B. | $\frac{{{x^2}-1}}{x-1}=\frac{{{{(x-1)}^2}}}{x-1}=x-1$ | ||
| C. | $\frac{{{x^2}-1}}{x-1}=\frac{(x+1)(x-1)}{x-1}=x+1$ | D. | $\frac{{{x^2}-1}}{x-1}=\frac{(x+1)(x-1)}{x-1}=\frac{1}{x+1}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
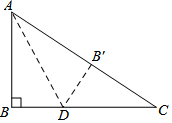 如圖所示,有一塊直角三角形紙片,兩直角邊AB=6,BC=8,將三角形ABC折疊,使AB落在斜邊AC上得到線段AB',折痕為AD,則BD的長為3.
如圖所示,有一塊直角三角形紙片,兩直角邊AB=6,BC=8,將三角形ABC折疊,使AB落在斜邊AC上得到線段AB',折痕為AD,則BD的長為3.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 4 | B. | 1 | C. | $\frac{1}{4}$ | D. | ±$\frac{1}{4}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com