Question

19．屈原食品公司接到一批粽子生產任務，按要求在15天內完成，約定這批粽子的出廠價為每只5元．為按時完成任務，該企業招收了新工人，設新工人小明第x天生產的粽子數量為n只，n與x滿足如下關系式：$\left\{\begin{array}{l}n=45x\\ n=30x+90\end{array}\right.$$\begin{array}{l}（0＜x≤5）\\（5＜x≤15）\end{array}$．
（1）小明第幾天生產的粽子數量為390只？
（2）設第x天每只粽子的成本是y元，y與x之間的關系的函數圖象如圖所示．若小明第x天的凈利潤為w元，試求w與x之間的函數表達式，并求出第幾天的凈利潤最大？最大值是多少元？（提示：凈利潤=出廠價-成本）

Answer 1

分析 （1）把n=390代入n=30x+90，解方程即可求得； 
（2）根據圖象求得成本y與x之間的關系，然后根據：凈利潤=（出廠價-成本價）×銷售量，結合x的范圍整理即可得到W與x的關系式，再根據一次函數的增減性和二次函數的增減性解答．

解答 解：（1）∵45×5=225＜390，
∴30x+90=390，
解得：x=10，
答：小明第10天生產的粽子數量為390只；

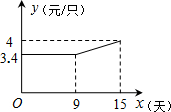
（2）由圖象可知，當0≤x≤9時，y=3.4；
當9＜x≤15時，設y=kx+b，
將（9，3.4）、（15，4）代入，得：$\left\{\begin{array}{l}{9k+b=3.4}\\{15k+b=4}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=0.1}\\{b=2.5}\end{array}\right.$，
∴y=0.1x+2.5；
①當0≤x≤5時，w=（5-3.4）×45x=72x，
∵w隨x的增大而增大，
∴當x=5時，w取得最大值，w_最大=360元；
②當5＜x≤9時，w=（5-3.4）（30x+90）=48x+144，
∵w隨x的增大而增大，
∴當x=9時，w取得最大值，w_最大=576元；
③當9＜x≤15時，w=[5-（0.1x+2.5）]（30x+90）
=-3x²+66x-225
=-3（x-11）²+138，
∴當x=11時，w取得最大值，w_最大=138元；
綜上，當x=9時，w取得最大值，w_最大=576元，
答：第9天的凈利潤最大，最大值是576元．

點評 本題考查的是二次函數在實際生活中的應用，主要是利用二次函數的增減性求最值問題，利用一次函數的增減性求最值，難點在于讀懂題目信息，列出相關的函數關系式．