

分析 (1)①只要證明∠KNM=∠KMN=80°,即可解決問題.
②如圖1中,當點B與點D重合時,△MKN的面積最大,設DM=x.根據勾股定理列出方程即可解決問題.
(2)①結論:四邊形KPMN是平行四邊形.只要證明KN=PM,KN∥PM即可.
②當點D與M重合,點B與點K重合時,S最大,設BD=B′D=BD′=x,A′P=C′N=y,由題意$\left\{\begin{array}{l}{2x+Y=5}\\{{x}^{2}=1+{y}^{2}}\end{array}\right.$,解方程組即可.當MK⊥A′B′時,根據垂線段最短可知,MK的最小值為1,此時S的最小值為1.
③當∠NMB′=60°或120°時,四邊形KPMN是菱形.求出菱形的高和邊長即可.
解答 解:(1)①如圖2中,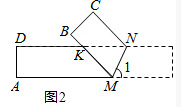
∵DN∥AM,
∴∠DNM=∠1=80°,
∵∠KMN=∠1=80°,
∴∠NKM=180°-∠KNM-∠KMN=20°,
故答案為20°.
②如圖1中,當點B與點D重合時,△MKN的面積最大,設DM=x.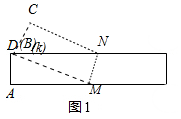
在Rt△AMD中,AD=1,AM=5-x,DM=x,
∴x2=12+(5-x)2,
∴x=$\frac{13}{5}$,
由①可知∠DMN=∠DNM,
∴KN=DM=$\frac{13}{5}$,
∴△KNM的面積最大值為$\frac{1}{2}$•$\frac{13}{5}$•1=$\frac{13}{10}$.
故答案為$\frac{13}{10}$.
(2)①結論:四邊形KPMN是平行四邊形.
理由:如圖3中,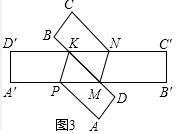
∵A′B′∥C′D′,
∴∠KNM=∠NMB′=∠NMK,
∴KN=KM,同理可證KM=PM,
∴KN=PM,∵KN∥PM,
∴四邊形KPMN是平行四邊形.
②如圖4中,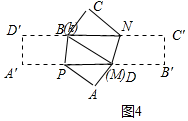
當點D與M重合,點B與點K重合時,S最大.設BD=B′D=BD′=x,A′P=C′N=y,
由題意$\left\{\begin{array}{l}{2x+Y=5}\\{{x}^{2}=1+{y}^{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{10-\sqrt{22}}{3}}\\{y=\frac{2\sqrt{22}-5}{3}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{10+\sqrt{22}}{3}}\\{y=\frac{-5-2\sqrt{22}}{3}}\end{array}\right.$(舍棄).
∴NK=$\frac{10-\sqrt{22}}{3}$,
∴S的最大值=$\frac{10-\sqrt{22}}{3}$.
當MK⊥A′B′時,根據垂線段最短可知,MK的最小值為1,此時S的最小值為1.
③四邊形KPMN能成為某種特殊四邊形,當∠NMB′=60°或120°時,四邊形KPMN是菱形.
此時菱形的高為1,邊長為$\frac{2\sqrt{3}}{3}$,所以S=$\frac{2\sqrt{3}}{3}$.
點評 本題考查四邊形綜合題、平行四邊形的性質、勾股定理、二元二次方程組、菱形的判定和性質等知識,第一個問題中的②解題的關鍵是正確尋找點B的位置,第二個問題中的②的解題關鍵是學會利用方程組解決問題,屬于中考壓軸題.


科目:初中數學 來源: 題型:選擇題
| A. | a=2,b=3 | B. | a=-2,b=-3 | C. | a=2或-2,b=3 | D. | a=0,b=3 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 0.06=6×10-3 | B. | -0.000026=-2.6×10-7 | ||
| C. | 168000=1.68×106 | D. | 28000000=2.8×107 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | -3與$-\frac{1}{3}$ | B. | |-3|與3 | C. | $|{-\frac{1}{3}}|$與$-\frac{1}{3}$ | D. | $-\frac{1}{3}$與$-|{-\frac{1}{3}}|$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
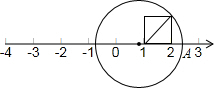 如圖所示,以數軸的單位長度線段為邊作一個正方形,以數軸上表示數1的點為圓心,正方形對角線長為半徑畫弧,交數軸正半軸于點A,則點A表示的數是( )
如圖所示,以數軸的單位長度線段為邊作一個正方形,以數軸上表示數1的點為圓心,正方形對角線長為半徑畫弧,交數軸正半軸于點A,則點A表示的數是( )| A. | $\sqrt{2}$ | B. | $1+\sqrt{2}$ | C. | 2.4 | D. | 2.3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com