
 ��֪����D��AB�ǡ�O��ֱ����ֱ��l����O��C��D���c(di��n)��AE��l��BF��l��E��F�Ǵ��㣬���C��EC=DF��
��֪����D��AB�ǡ�O��ֱ����ֱ��l����O��C��D���c(di��n)��AE��l��BF��l��E��F�Ǵ��㣬���C��EC=DF�� ���� �^(gu��)�c(di��n)O��OM��CD���c(di��n)M������(j��)����������֪CM=DM������AE��l��OM��l��BF��l�ɵó�AE��OM��BF���ٸ���(j��)AB�ǡ�O��ֱ����֪OA=OB����OM������AEFB����λ��������EM-CM=FM-DM���ɵó��Y(ji��)Փ��
��� 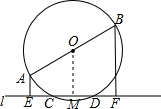 �C�����^(gu��)�c(di��n)O��OM��CD���c(di��n)M��
�C�����^(gu��)�c(di��n)O��OM��CD���c(di��n)M��
��OM��CD��
��CM=DM��
��AE��l��OM��l��BF��l��
��AE��OM��BF��
��AB�ǡ�O��ֱ����
��OA=OB��
��OM������AEFB�������
��EM=FM
��EM-CM=FM-DM����EC=DF
�c(di��n)�u(p��ng) ���}������Ǵ�������������(j��)�}�������o���������ô���������������λ����������ǽ����}���P(gu��n)�I��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
 ��D����ֱ������(bi��o)ϵ�У���֪A��-4��$\frac{1}{2}$����B��-1��2����һ�κ���(sh��)y=kx+b�c����������(sh��)y=$\frac{m}{x}$��m��0���D��ăɂ�(g��)���c(di��n)��AC��x�S��C��BD��y�S��D��
��D����ֱ������(bi��o)ϵ�У���֪A��-4��$\frac{1}{2}$����B��-1��2����һ�κ���(sh��)y=kx+b�c����������(sh��)y=$\frac{m}{x}$��m��0���D��ăɂ�(g��)���c(di��n)��AC��x�S��C��BD��y�S��D���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
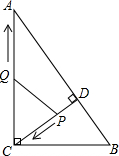 ��D����Rt��ABC�У���ACB=90�㣬AC=8��BC=6��CD��AB���c(di��n)D���c(di��n)P���c(di��n)D���l(f��)���ؾ���DC���c(di��n)C�\(y��n)��(d��ng)���c(di��n)Q���c(di��n)C���l(f��)���ؾ���CA���c(di��n)A�\(y��n)��(d��ng)�����c(di��n)ͬ�r(sh��)���l(f��)���ٶȶ���ÿ��1��(g��)��λ�L(zh��ng)�ȣ���(d��ng)�c(di��n)P�\(y��n)��(d��ng)���c(di��n)C�r(sh��)�����c(di��n)��ֹͣ���O(sh��)�\(y��n)��(d��ng)�r(sh��)�g��t�룮
��D����Rt��ABC�У���ACB=90�㣬AC=8��BC=6��CD��AB���c(di��n)D���c(di��n)P���c(di��n)D���l(f��)���ؾ���DC���c(di��n)C�\(y��n)��(d��ng)���c(di��n)Q���c(di��n)C���l(f��)���ؾ���CA���c(di��n)A�\(y��n)��(d��ng)�����c(di��n)ͬ�r(sh��)���l(f��)���ٶȶ���ÿ��1��(g��)��λ�L(zh��ng)�ȣ���(d��ng)�c(di��n)P�\(y��n)��(d��ng)���c(di��n)C�r(sh��)�����c(di��n)��ֹͣ���O(sh��)�\(y��n)��(d��ng)�r(sh��)�g��t�룮�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
 ��D���ڡ�ABC�У�AB=AC��EF��AB���c(di��n)E����BC�c�c(di��n)D����AC�����L(zh��ng)�����c(di��n)F����BE=CF�����C��DE=DF��
��D���ڡ�ABC�У�AB=AC��EF��AB���c(di��n)E����BC�c�c(di��n)D����AC�����L(zh��ng)�����c(di��n)F����BE=CF�����C��DE=DF���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ��x���}
 �����Ă�(g��)ˇ�g(sh��)���У����S��(du��)�Q�D�εĂ�(g��)��(sh��)�ǣ�������
�����Ă�(g��)ˇ�g(sh��)���У����S��(du��)�Q�D�εĂ�(g��)��(sh��)�ǣ�������| A�� | 1��(g��) | B�� | 2��(g��) | C�� | 3��(g��) | D�� | 4��(g��) |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
 ��D��ʾ����֪��ACB=90�㣬��ADC=90�㣬�D�л��ഹֱ�ľ�����AC��BC��CD��AB��
��D��ʾ����֪��ACB=90�㣬��ADC=90�㣬�D�л��ഹֱ�ľ�����AC��BC��CD��AB���鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com