
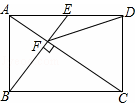
 如圖,點E是矩形ABCD的邊AD的中點,且BE⊥AC于點F,則下列結論中錯誤的是( )
如圖,點E是矩形ABCD的邊AD的中點,且BE⊥AC于點F,則下列結論中錯誤的是( )| A. | AF=$\frac{1}{2}$CF | B. | ∠DCF=∠DFC | ||
| C. | 圖中與△AEF相似的三角形共有4個 | D. | tan∠CAD=$\frac{\sqrt{2}}{2}$ |
分析 由AE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,又AD∥BC,所以$\frac{AE}{BC}$=$\frac{AF}{FC}$=$\frac{1}{2}$,故A正確,不符合題意;
過D作DM∥BE交AC于N,得到四邊形BMDE是平行四邊形,求出BM=DE=$\frac{1}{2}$BC,得到CN=NF,根據線段的垂直平分線的性質可得結論,故B正確,不符合題意;
根據相似三角形的判定即可求解,故C正確,不符合題意;
由△BAE∽△ADC,得到CD與AD的大小關系,根據正切函數可求tan∠CAD的值,故D錯誤,符合題意.
解答 解: A、∵AD∥BC,
A、∵AD∥BC,
∴△AEF∽△CBF,
∴$\frac{AE}{BC}$=$\frac{AF}{FC}$,
∵AE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,
∴$\frac{AF}{FC}$=$\frac{1}{2}$,故A正確,不符合題意;
B、過D作DM∥BE交AC于N,
∵DE∥BM,BE∥DM,
∴四邊形BMDE是平行四邊形,
∴BM=DE=$\frac{1}{2}$BC,
∴BM=CM,
∴CN=NF,
∵BE⊥AC于點F,DM∥BE,
∴DN⊥CF,
∴DF=DC,
∴∠DCF=∠DFC,故B正確,不符合題意;
C、圖中與△AEF相似的三角形有△ACD,△BAF,△CBF,△CAB,△ABE共有5個,故C錯誤.
D、設AD=a,AB=b由△BAE∽△ADC,有$\frac{b}{a}$=$\frac{\frac{a}{2}}{b}$.
∵tan∠CAD=$\frac{CD}{AD}$=$\frac{b}{a}$=$\frac{\sqrt{2}}{2}$,故D正確,不符合題意.
故選C.
點評 本題考查了相似三角形的判定和性質,矩形的性質,圖形面積的計算,正確的作出輔助線是解題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
 在下列有理數運算中,不能借助下面數軸解釋的是( )
在下列有理數運算中,不能借助下面數軸解釋的是( )| A. | (-3)+(-3)=-6 | B. | (-3)×2=-6 | C. | 2×(-3)=-6 | D. | 3×(-2)=-6 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| 每天零花錢(元) | 0 | 5 | 10 | 15 | 20 |
| 人數 | 2 | 3 | 2 | 6 | 2 |
| A. | 眾數是20元 | B. | 平均數是11元 | C. | 極差是15元 | D. | 中位數是10元 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
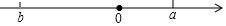
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com