
【題目】若將拋物線y=mx2﹣x﹣m(m≠0)在直線x=﹣1與直線x=1之間的部分記作圖象C,對于圖象C上任意一點P(a,b)均有﹣1≤b≤1成立,則m的取值范圍是___.
【答案】﹣![]() ≤m≤
≤m≤![]() 且m≠0.
且m≠0.
【解析】
要使對于圖象C上任意一點P(a,b)均有-1≤b≤1成立,只需在給定區域內,y的最大值都滿足條件即可;分m>0和m<0兩種情況討論,當m>0時,在分①當0<![]() <1時,②當
<1時,②當![]() ≥1時;當m<0時再分①當-1<
≥1時;當m<0時再分①當-1<![]() <0時,②當
<0時,②當![]() ≤-1時,最后將解的情況綜合.
≤-1時,最后將解的情況綜合.
解:y=mx2﹣x﹣m (m≠0)的對稱軸是x=![]() ,
,
(1)當m>0時,![]() >0,
>0,
①當0<![]() <1時,即m>
<1時,即m>![]() ,
,
此時當x=﹣1時有最大值1;
此時當x=![]() 時有最小值
時有最小值![]() ,
,
![]() =﹣1,
=﹣1,
∴m=![]() ,
,
②當![]() ≥1時,即0<m≤
≥1時,即0<m≤![]() ,
,
此時當x=﹣1時有最大值1;
此時當x=1時有最小值﹣1;
∴0<m≤![]() ;
;
(2)當m<0時,![]() <0,
<0,
①當﹣1<![]() <0時,即m<
<0時,即m<![]() ,
,
此時當x=![]() 時,y有最大值
時,y有最大值![]() ,
,
∴![]() =1,
=1,
∴m=![]() ,
,
當x=1時有最小值﹣1,
∴m=![]() ,
,
②當![]() ≤﹣1時,即
≤﹣1時,即![]() ≤m<0,
≤m<0,
此時當x=﹣1時有最大值1;
當x=1時有最小值﹣1;
∴![]() ≤m<0,
≤m<0,
綜上所述,![]() ≤m≤
≤m≤![]() 且m≠0.
且m≠0.


科目:初中數學 來源: 題型:
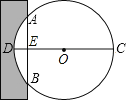
【題目】《九章算術》是我國古代數學成就的杰出代表作,書中記載:“今有中,不知大小.以鋸鋸之,深1寸,鋸道長1尺,問經幾何?“其意思為:“如圖,今有一圓形木材在墻中,不知其大小用鋸子去鋸這個木材,鋸口深DE=1寸,鋸道長AB=10寸,問這塊圓形木材的直徑是多少?”
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某旅游風景區出售一種紀念品,該紀念品的成本為![]() 元/個,這種紀念品的銷售價格為
元/個,這種紀念品的銷售價格為![]() (元/個)與每天的銷售數量
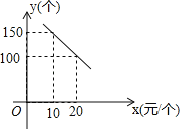
(元/個)與每天的銷售數量![]() (個)之間的函數關系如圖所示.
(個)之間的函數關系如圖所示.
(1)求![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(2)銷售價格定為多少時,每天可以獲得最大利潤?并求出最大利潤.
(3)“十一”期間,游客數量大幅增加,若按八折促銷該紀念品,預計每天的銷售數量可增加![]() ,為獲得最大利潤,“十一”假期該紀念品打八折后售價為多少?
,為獲得最大利潤,“十一”假期該紀念品打八折后售價為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司生產的商品的市場指導價為每件150元,公司的實際銷售價格可以浮動x個百分點(即銷售價格=150(1+x%)),經過市場調研發現,這種商品的日銷售量y(件)與銷售價格浮動的百分點x之間的函數關系為y=﹣2x+24.若該公司按浮動﹣12個百分點的價格出售,每件商品仍可獲利10%.
(1)求該公司生產銷售每件商品的成本為多少元?
(2)當實際銷售價格定為多少元時,日銷售利潤為660元?(說明:日銷售利潤=(銷售價格一成本)×日銷售量)
(3)該公司決定每銷售一件商品就捐贈a元利潤(a≥1)給希望工程,公司通過銷售記錄發現,當價格浮動的百分點大于﹣2時,扣除捐贈后的日銷售利潤隨x增大而減小,直接寫出a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
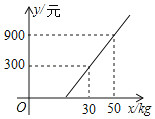
【題目】某旅客攜帶xkg的行李乘飛機,登機前,旅客可選擇托運或快遞行李,托運費y1(元)與行李重量xkg的對應關系由如圖所示的一次函數圖象確定,下表列出了快遞費y2(元)與行李重量xkg的對應關系.
行李的重量xkg | 快遞費 |
不超過1kg | 10元 |
超過1kg但不超過5kg的部分 | 3元/kg |
超過5kg但不超過15kg的部分 | 5元/kg |
(1)如果旅客選擇單托運,求可攜帶的免費行李的最大重量為多少kg?
(2)如果旅客選擇快遞,當1<x≤15時,直接寫出快遞費y2(元)與行李的重量xkg之間的函數關系式;
(3)某旅客攜帶25kg的行李,設托運mkg行李(10≤m<24,m為正整數),剩下的行李選擇快遞,當m為何值時,總費用y的值最小?并求出其最小值是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明同學在學習與圓有關的角時了解到:在同圓或等圓中,同弧(或等弧)所對的圓周角相等.如圖,點A、B、C、D均為⊙O上的點,則有∠C=∠D.
小明還發現,若點E在⊙O外,且與點D在直線AB同側,則有∠D >∠E. 請你參考小明得出的結論,解答下列問題:
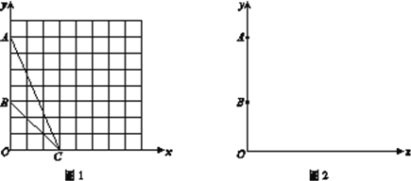
(1)如圖1,在平面直角坐標系xOy中,點A的坐標為(0,7),點B的坐標為(0,3),點C的坐標為(3,0) .①在圖1中作出△ABC的外接圓(保留必要的作圖痕跡,不寫作法);
②若在![]() 軸的正半軸上有一點D,且∠ACB =∠ADB,則點D的坐標為________;
軸的正半軸上有一點D,且∠ACB =∠ADB,則點D的坐標為________;
(2) 如圖2,在平面直角坐標系xOy中,點A的坐標為(0,m),點B的坐標為(0,n),其中m>n>0.點P為![]() 軸正半軸上的一個動點,當∠APB達到最大時,直接寫出此時點P的坐標.
軸正半軸上的一個動點,當∠APB達到最大時,直接寫出此時點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=x2﹣3x+m(m為常數)的圖象與x軸的一個交點為(1,0),則關于x的一元二次方程x2﹣3x+m=0的兩實數根是( )
A. x1=1,x2=﹣1B. x1=1,x2=3C. x1=1,x2=2D. x1=1,x2=3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com