
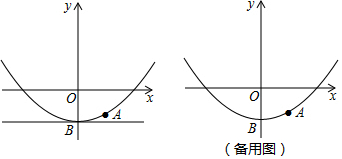
分析 (1)利用待定系數(shù)法即可解決問題.
(2)只要證明圓心C到直線l的距離等于圓的半徑即可.
(3))①由(2)可知,若直線l與⊙C相切,則:2t-$\frac{5}{8}$=t+$\frac{5}{8}$,t=$\frac{5}{4}$;由此即可判斷當(dāng)0<t<$\frac{5}{4}$時,直線l與⊙C相交;
②因為0<t<$\frac{5}{4}$時,圓心C到直線l的距離為d=|2t-$\frac{5}{8}$|,又半徑為r=t+$\frac{5}{8}$,所以a2=4(r2-d2)=4[(t+$\frac{5}{8}$)2-|2t-$\frac{5}{8}$|2]=-12t2+15t,根據(jù)二次函數(shù)的性質(zhì)即可解決問題.
解答 解:(1)將點A(1,-$\frac{3}{4}$)代入y=$\frac{1}{4}$x2+m中,得:
m=-1,
∴拋物線的解析式:y=$\frac{1}{4}$x2-1;
(2)結(jié)論:直線l與⊙C始終保持相切.
理由:將P點縱坐標(biāo)代入(1)的解析式,得:
$\frac{1}{4}$a2-1=-$\frac{3}{4}$+2t,a=$\sqrt{8t+1}$,
∴P( $\sqrt{8t+1}$,-$\frac{3}{4}$+2t),
∴圓心C( $\frac{\sqrt{8t+1}}{2}$,-$\frac{3}{8}$+t),
∴點C到直線l的距離:-$\frac{3}{8}$+t-(-1)=t+$\frac{5}{8}$;
而OP2=8t+1+(-$\frac{3}{4}$+2t)2,得OP=2t+$\frac{5}{4}$,半徑OC=t+$\frac{5}{8}$;
∴直線l與⊙C始終保持相切.
(3)①由(1)可知,若直線l與⊙C相切,則:2t-$\frac{5}{8}$=t+$\frac{5}{8}$,t=$\frac{5}{4}$;
∴當(dāng)0<t<$\frac{5}{4}$時,直線l與⊙C相交;
②∵0<t<$\frac{5}{4}$時,圓心C到直線l的距離為d=|2t-$\frac{5}{8}$|,又半徑為r=t+$\frac{5}{8}$,
∴a2=4(r2-d2)=4[(t+$\frac{5}{8}$)2-|2t-$\frac{5}{8}$|2]=-12t2+15t,
∴t=$\frac{5}{8}$時,a的平方取得最大值為 $\frac{75}{16}$.
點評 本題考查二次函數(shù)綜合題、直線與圓的位置關(guān)系等知識,解題的關(guān)鍵是靈活運(yùn)用直線與圓相切的判定方法,在處理此類問題時,要注意尋找關(guān)鍵點以及分段進(jìn)行討論,以免出現(xiàn)漏解.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源:2017屆遼寧省丹東市九年級第一次模擬考試數(shù)學(xué)試卷(解析版) 題型:單選題
如圖,在△ABC中,AD和BE是高,∠ABE=45°,點F是AB的中點,AD與FE、BE分別交于點G、H,∠CBE=∠BAD.有下列結(jié)論:①FD=FE;②AH=2CD;③BC•AD=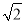 AE2;④∠DFE=2∠DAC ;⑤若連接CH,則CH∥EF.其中正確的個數(shù)為( )
AE2;④∠DFE=2∠DAC ;⑤若連接CH,則CH∥EF.其中正確的個數(shù)為( )
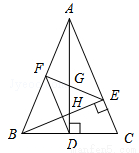
A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com