
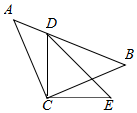
 如圖,AC=BC且AC⊥BC,點D在AB上,DC=EC且DC⊥EC.
如圖,AC=BC且AC⊥BC,點D在AB上,DC=EC且DC⊥EC.分析 連接BE,由等腰直角三角形的性質得出∠A=∠ABC=45°,∠ACB=∠DCE=90°,證出∠ACD=∠BCE,由SAS證明△ACD≌△BCE,得出BE=AD,∠EBC=∠A=45°,求出∠DBE=90°,在Rt△BDE和Rt△CDE中,由勾股定理得出BD2+BE2=CD2+EC2,即可得出結論.
解答 證明:連接BE,如圖所示: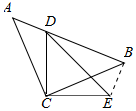
∵AC=BC且AC⊥BC,DC=EC且DC⊥EC,
∴∠A=∠ABC=45°,∠ACB=∠DCE=90°,
∴∠ACB-∠BCD=∠DCE-∠BCD,
即∠ACD=∠BCE,
在△ACD和△BCE中,$\left\{\begin{array}{l}{AC=BC}&{\;}\\{∠ACD=∠BCE}&{\;}\\{DC=EC}&{\;}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴BE=AD,∠EBC=∠A=45°,
∴∠DBE=45°+45°=90°,
在Rt△BDE和Rt△CDE中,DE2=BD2+BE2,DE2=CD2+EC2,
∴BD2+BE2=CD2+EC2,
又∵AD=BE,CD=EC,
∴AD2+BD2=2EC2.
點評 本題考查了勾股定理、等腰直角三角形的性質、全等三角形的判定與性質;熟練掌握勾股定理,證明三角形全等是解決問題的關鍵.


 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案科目:初中數學 來源: 題型:選擇題
| A. | -0.07205 | B. | -0.03344 | C. | -0.07205 | D. | -0.003344 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 若$\sqrt{x-1}$+$\sqrt{1-x}$=y+4,則xy的平方根為1 | B. | 3-2$\sqrt{2}$的絕對值是2$\sqrt{2}$-3 | ||
| C. | 若$\sqrt{{a}^{2}b}$=-a$\sqrt{b}$成立,則a≤0且b≥0 | D. | 若$\sqrt{(1-a)^{2}}$+$\sqrt{(a-3)^{2}}$=2,則a≥3 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
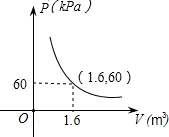 某氣球內充滿了一定質量的氣體,當溫度不變時,氣球內氣體的氣壓p(單位:kPa)是氣體體積V(單位:m3)的反比例函數,其圖象如圖.當氣球內的氣壓大于120kPa時,氣球將爆炸.為了安全起見,氣球的體積應( )
某氣球內充滿了一定質量的氣體,當溫度不變時,氣球內氣體的氣壓p(單位:kPa)是氣體體積V(單位:m3)的反比例函數,其圖象如圖.當氣球內的氣壓大于120kPa時,氣球將爆炸.為了安全起見,氣球的體積應( )| A. | 不小于$\frac{5}{4}$ m3 | B. | 小于$\frac{5}{4}$ m3 | C. | 不小于$\frac{4}{5}$ m3 | D. | 小于$\frac{4}{5}$ m3 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (3,8) | B. | (3,-8) | C. | (-8,-3) | D. | (-4,-6) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com