
【題目】某工廠安排甲、乙兩個運輸隊各從倉庫調運物資300噸,兩隊同時開始工作,甲運輸隊工作3天后因故停止,2天后重新開始工作,由于工廠調離了部分工人,甲運輸的工作效率降低到原來的![]() 甲、乙運輸隊調運物資的數量
甲、乙運輸隊調運物資的數量![]() 噸
噸![]() 與甲工作時間
與甲工作時間![]() 天
天![]() 的函數圖象如圖所示.
的函數圖象如圖所示.
![]() ______;
______;![]() ______.
______.
![]() 求甲運輸隊重新開始工作后,甲運輸隊調運物資的數量
求甲運輸隊重新開始工作后,甲運輸隊調運物資的數量![]() 噸
噸![]() 與工作時間
與工作時間![]() 天
天![]() 的函數關系式;
的函數關系式;
![]() 直接寫出乙運輸隊比甲運輸隊多運50噸物資時x的值.
直接寫出乙運輸隊比甲運輸隊多運50噸物資時x的值.

【答案】(1)5;11 (2)解析式為![]() (3)
(3)![]() 或9
或9
【解析】
(1)根據甲隊休息了2天可知,a=3+2=5,因為重新工作后甲運輸的工作效率降低到原來的![]() ,所以原來3天調運150噸,現在需6天調運150噸,即可得到b=5+6=11;
,所以原來3天調運150噸,現在需6天調運150噸,即可得到b=5+6=11;
(2)設函數關系式為![]() ,根據圖中函數圖象的坐標,用待定系數法即可求得函數解析式;
,根據圖中函數圖象的坐標,用待定系數法即可求得函數解析式;
(3)根據題意得到乙運輸隊調運物資的數量![]() 噸
噸![]() 與工作時間
與工作時間![]() 天
天![]() 的函數關系式:
的函數關系式:![]() ,然后分乙隊未完成運輸和完成運輸后兩種情況,分別與甲隊的函數關系式列出方程求解即可.
,然后分乙隊未完成運輸和完成運輸后兩種情況,分別與甲隊的函數關系式列出方程求解即可.
(1)∵甲運輸隊工作3天后因故停止,2天后重新開始工作,
∴![]() (天),
(天),
∵甲運輸的工作效率降低到原來的![]() ,
,
∴原來3天調運150噸,現在需6天調運150噸.
∴![]() (天);
(天);
![]() 設函數關系式為
設函數關系式為![]() ,
,
![]() 圖象過
圖象過![]() ,
,![]()
∴![]() ,
,
解得:![]() ,
,
![]() 解析式為
解析式為![]() ;
;
![]() 由題意得:乙運輸隊調運物資的數量
由題意得:乙運輸隊調運物資的數量![]() 噸
噸![]() 與工作時間
與工作時間![]() 天
天![]() 的函數關系式:
的函數關系式:![]() ,
,
①若乙運輸隊調運物資沒有完成,
∵乙運輸隊比甲運輸隊多運50噸物資,
∴![]() ,
,
解得:![]() ,
,
②當乙運輸隊運輸完物資后,
![]() 乙運輸隊比甲運輸隊多運50噸物資,
乙運輸隊比甲運輸隊多運50噸物資,
∴![]() ,
,
解得:![]() ;
;
故![]() 6或9.
6或9.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在邊長為4的正方形ABCD中,動點P從A點出發,以每秒1個單位長度的速度沿AB向B點運動,同時動點Q從B點出發,以每秒2個單位長度的速度沿BC→CD方向運動,當P運動到B點時,P、Q兩點同時停止運動.設P點運動的時間為t,△APQ的面積為S,則S與t的函數關系的圖象是【 】

查看答案和解析>>
科目:初中數學 來源: 題型:
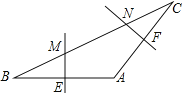
【題目】如圖,在△ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分線交BC于點M,交AB于點E,AC的垂直平分線交BC于點N,交AC于點F,則MN的長為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB = AC,點D是邊BC的中點,過點A、D分別作BC與AB的平行線,相交于點E,連結EC、AD.
求證:四邊形ADCE是矩形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,任意一個有理數與無理數的和為無理數,任意一個不為零的有理數與一個無理數的積為無理數,而零與無理數的積為零.由此可得:如果mx+n=0,其中m、n為有理數,x為無理數,那么m=0且n=0.
(1)如果![]() ,其中a、b為有理數,那么a= ,b= .
,其中a、b為有理數,那么a= ,b= .
(2)如果![]() ,其中a、b為有理數,求a+2b的值.
,其中a、b為有理數,求a+2b的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
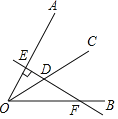
【題目】已知∠AOB=60°,OC是∠AOB的平分線,點D為OC上一點,過D作直線DE⊥OA,垂足為點E,且直線DE交OB于點F,如圖所示,若DE=1,則DF=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:對于二次三項式a2+2ab+b2,能直接用完全平方公式進行因式分解,得到結果為(a+b)2.而對于二次三項式a2+4ab﹣5b2,就不能直接用完全平方公式了,但我們可采用下述方法:
a2+4ab﹣5b2=a2+4ab+4b2﹣4b2﹣5b2=(a+2b)2﹣9b2,
=(a+2b﹣3b)(a+2b+3b)=(a﹣b)(a+5b).
像這樣把二次三項式分解因式的方法叫做添(拆)項法.
解決問趣:
(1)請利用上述方法將二次三項式a2+6ab+8b2分解因式;
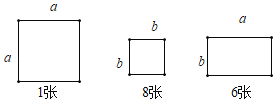
(2)如圖,邊長為a的正方形紙片1張,邊長為b的正方形紙片8張,長為a,寬為b的長方形紙片6張,這些紙片可以拼成一個不重疊,無空隙的長方形圖案,請畫出示意圖;
(3)已知x>0,且x≠2,試比較分式![]() 與
與![]() 的大小.
的大小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是李剛同學在一次測驗中解答的數學題:
①若![]() ,則
,則![]() ,
,
②方程![]() 的解為
的解為![]() ,
,
③若![]() 兩根的倒數和等于
兩根的倒數和等于![]() ,則
,則![]() ,
,
④若![]() 是方程
是方程![]() 的解,則
的解,則![]() 或
或![]() .
.
其中答對的是________(填序號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com