
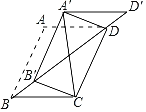
【題目】如圖,在邊長為1的菱形ABCD中,∠ABC=60°,將△ABD沿射線BD的方向平移得到△A'B'D',分別連接A'C,A'D,B'C,則A'C+B'C的最小值為_____.
【答案】![]()
【解析】
根據菱形和平移的性質得出四邊形A′B′CD是平行四邊形,進而得出A′D=B′C,根據最短路徑問題的步驟求解即可得出答案.
解:∵在邊長為1的菱形ABCD中,∠ABC=60°,
∴AB=CD=1,∠ABD=30°,
∵將△ABD沿射線BD的方向平移得到△A'B'D',
∴A′B′=AB=1,A′B′∥AB,
∵四邊形ABCD是菱形,
∴AB=CD,AB∥CD,
∴∠BAD=120°,
∴A′B′=CD,A′B′∥CD,
∴四邊形A′B′CD是平行四邊形,
∴A′D=B′C,
∴A'C+B'C的最小值=A′C+A′D的最小值,
∵點A′在過點A且平行于BD的定直線上,
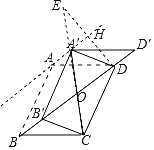
∴作點D關于定直線的對稱點E,連接CE交定直線于A′,
則CE的長度即為A'C+B'C的最小值,
∵∠A′AD=∠ADB=30°,AD=1,
∴∠ADE=60°,DH=EH=![]() AD=
AD=![]() ,
,
∴DE=1,
∴DE=CD,
∵∠CDE=∠EDB′+∠CDB=90°+30°=120°,
∴∠E=∠DCE=30°,
∴CE=![]() CD=
CD=![]() .
.
故答案為:![]() .
.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案科目:初中數學 來源: 題型:
【題目】某商店購買60件A商品和30件B商品共用了1080元,購買50件A商品和20件B商品共用了880元.
(1)A、B兩種商品的單價分別是多少元?
(2)已知該商店購買B商品的件數比購買A商品的件數的2倍少4件,如果需要購買A、B兩種商品的總件數不少于32件,且該商店購買的A、B兩種商品的總費用不超過296元,那么該商店有哪幾種購買方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
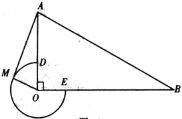
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以點
,以點![]() 為圓心,以
為圓心,以![]() 為半徑作優弧
為半徑作優弧![]() ,交
,交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() .點
.點![]() 在優弧
在優弧![]() 上從點
上從點![]() 開始移動,到達點
開始移動,到達點![]() 時停止,連接
時停止,連接![]() .
.
(1)當![]() 時,判斷
時,判斷![]() 與優弧
與優弧![]() 的位置關系,并加以證明;
的位置關系,并加以證明;
(2)當![]() 時,求點
時,求點![]() 在優弧
在優弧![]() 上移動的路線長及線段
上移動的路線長及線段![]() 的長.
的長.
(3)連接![]() ,設
,設![]() 的面積為
的面積為![]() ,直接寫出
,直接寫出![]() 的取值范圍.
的取值范圍.
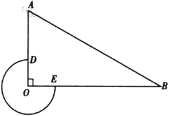
備用圖
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線![]() :
:![]() 與
與![]() 軸交于
軸交于![]() 兩點(
兩點(![]() 在
在![]() 的左側),與
的左側),與![]() 軸交于點
軸交于點![]() .
.
(1)求拋物線![]() 的解析式及
的解析式及![]() 兩點的坐標;
兩點的坐標;
(2)求拋物線![]() 的頂點坐標;
的頂點坐標;
(3)將拋物線![]() 向上平移3個單位長度,再向右平移
向上平移3個單位長度,再向右平移![]() 個單位長度,得到拋物線
個單位長度,得到拋物線![]() .①若拋物線
.①若拋物線![]() 的頂點在
的頂點在![]() 內,求
內,求![]() 的取值范圍;②若拋物線
的取值范圍;②若拋物線![]() 與線段
與線段![]() 只有一個交點,直接寫出
只有一個交點,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,半圓O的直徑AB=5cm,點M在AB上且AM=1cm,點P是半圓O上的動點,過點B作BQ⊥PM交PM(或PM的延長線)于點Q.設PM=xcm,BQ=ycm.(當點P與點A或點B重合時,y的值為0)小石根據學習函數的經驗,對函數y隨自變量x的變化而變化的規律進行了探究.下面是小石的探究過程,請補充完整:
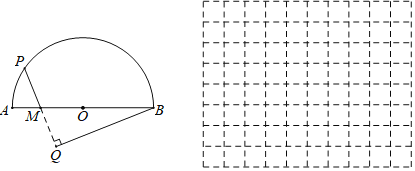
(1)通過取點、畫圖、測量,得到了x與y的幾組值,如下表:
x/cm | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm | 0 | 3.7 | ______ | 3.8 | 3.3 | 2.5 | ______ |
(2)建立平面直角坐標系,描出以補全后的表中各對對應值為坐標的點,畫出該函數的圖象;
(3)結合畫出的函數圖象,解決問題:當BQ與直徑AB所夾的銳角為60°時,PM的長度約為______cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
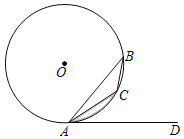
【題目】如圖,直線AD經過⊙O上的點A,△ABC為⊙O的內接三角形,并且∠CAD=∠B.
(1)判斷直線AD與⊙O的位置關系,并說明理由;
(2)若∠CAD=30°,⊙O的半徑為1,求圖中陰影部分的面積.(結果保留π)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】A、B兩所學校的學生都參加了某次體育測試,成績均為7﹣10分,且為整數.亮亮分別從這兩所學校各隨機抽取一部分學生的測試成績,共200份,并繪制了如下尚不完整的統計圖.
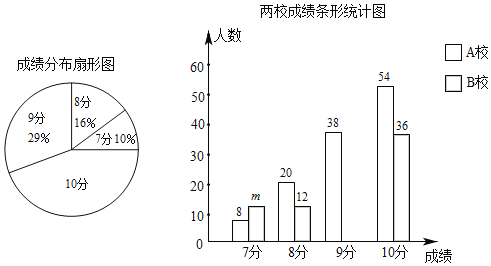
(1)這200份測試成績的中位數是 分,m= ;
(2)補全條形統計圖;扇形統計圖中,求成績為10分所在扇形的圓心角的度數.
(3)亮亮算出了“1名A校學生的成績被抽到”的概率是![]() ,請你估計A校成績為8分的學生大約有多少名.
,請你估計A校成績為8分的學生大約有多少名.
查看答案和解析>>
科目:初中數學 來源: 題型:
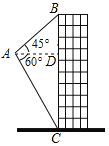
【題目】如圖,航拍無人機從A處測得一幢建筑物頂部B的仰角為45°,測得底部C的俯角為60°,此時航拍無人機與該建筑物的水平距離AD為110m,那么該建筑物的高度BC約為_____m(結果保留整數,![]() ≈1.73).
≈1.73).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(6分)在一個不透明的口袋裝有三個完全相同的小球,分別標號為1、2、3.求下列事件的概率:
(1)從中任取一球,小球上的數字為偶數;
(2)從中任取一球,記下數字作為點A的橫坐標x,把小球放回袋中,再從中任取一球記下數字作為點A的縱坐標y,點A(x,y)在函數![]() 的圖象上.
的圖象上.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com