
【題目】拋物線![]() :
:![]() 與
與![]() 軸交于
軸交于![]() 兩點(
兩點(![]() 在
在![]() 的左側),與
的左側),與![]() 軸交于點
軸交于點![]() .
.
(1)求拋物線![]() 的解析式及
的解析式及![]() 兩點的坐標;
兩點的坐標;
(2)求拋物線![]() 的頂點坐標;
的頂點坐標;
(3)將拋物線![]() 向上平移3個單位長度,再向右平移
向上平移3個單位長度,再向右平移![]() 個單位長度,得到拋物線
個單位長度,得到拋物線![]() .①若拋物線
.①若拋物線![]() 的頂點在
的頂點在![]() 內,求
內,求![]() 的取值范圍;②若拋物線
的取值范圍;②若拋物線![]() 與線段
與線段![]() 只有一個交點,直接寫出
只有一個交點,直接寫出![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)①
;(3)①![]() ,②
,②![]() 或
或![]()
【解析】
(1)將點![]() 代入
代入![]() ,即可得到拋物線
,即可得到拋物線![]() 的解析式;在
的解析式;在![]() 中,令
中,令![]() ,即可得到
,即可得到![]() 兩點的坐標;
兩點的坐標;
(2)運用配方法,將解析式改寫成頂點式,即可得到頂點坐標;
(3)①先寫出平移后的解析式,求出頂點,再根據頂點在![]() 內,需滿足頂點需在
內,需滿足頂點需在![]() 軸下方,在直線
軸下方,在直線![]() 的右側,
的右側,![]() 的左側,列出關于
的左側,列出關于![]() 的不等式組,解出即可;
的不等式組,解出即可;
②分為拋物線![]() 和線段
和線段![]() 的唯一交點在拋物線對稱軸右側;拋物線
的唯一交點在拋物線對稱軸右側;拋物線![]() 和線段
和線段![]() 的唯一交點在拋物線對稱軸左側,且在點B的左側;拋物線
的唯一交點在拋物線對稱軸左側,且在點B的左側;拋物線![]() 和線段
和線段![]() 的唯一交點在拋物線對稱軸左側,點B為
的唯一交點在拋物線對稱軸左側,點B為![]() 和線段
和線段![]() 交點三種情況討論.
交點三種情況討論.
解:(1)∵將點![]() 代入
代入![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
∴拋物線![]() 的解析式為
的解析式為![]()
在![]() 中,令
中,令![]() ,得
,得![]() ,
,![]() ,
,
∵![]() 在
在![]() 的左側,∴
的左側,∴![]() ,
,![]()
(2)∵![]() 即
即![]() ,
,
∴拋物線![]() 的頂點坐標為
的頂點坐標為![]()
(3)①將拋物線![]() 平移后
平移后![]() 的解析式為:
的解析式為:![]() ,
,
![]() 頂點為(
頂點為(![]() ),
),
若要![]() 頂點在
頂點在![]() 內,則頂點需在
內,則頂點需在![]() 軸下方,在直線
軸下方,在直線![]() 的右側,
的右側,![]() 的左側,
的左側,

因為![]() ,所以,頂點必在
,所以,頂點必在![]() 軸下方,因為
軸下方,因為![]() ,所以頂點必在
,所以頂點必在![]() 的右側,
的右側,
設直線![]() 的解析式為
的解析式為![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() 解得
解得![]() ,
,
∴直線![]() 的解析式為
的解析式為![]()
當![]() 時,
時,![]() .
.
∴![]() ,
,![]() ,
,
又∵![]()
∴![]() 的取值范圍是
的取值范圍是![]()
②第1種情況,拋物線![]() 和線段
和線段![]() 的唯一交點在拋物線對稱軸右側,
的唯一交點在拋物線對稱軸右側,
則拋物線![]() 和直線
和直線![]() 只有一個交點,且頂點的橫坐標小于等于3,
只有一個交點,且頂點的橫坐標小于等于3,
聯立拋物線![]() 和直線
和直線![]() 解析式
解析式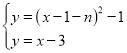 ,
,
則![]() 有兩個相等的根,且小于等于3,
有兩個相等的根,且小于等于3,
∴![]() ,且
,且![]() ,
,
∴![]() ;
;
第2種情況,拋物線![]() 和線段
和線段![]() 的唯一交點在拋物線對稱軸左側,且在點B的左側,
的唯一交點在拋物線對稱軸左側,且在點B的左側,
則點B在拋物線的上側,
即當![]() 時,
時,![]() ,解得
,解得![]() ;
;
第3種情況,拋物線![]() 和線段
和線段![]() 的唯一交點在拋物線對稱軸左側,點B為
的唯一交點在拋物線對稱軸左側,點B為![]() 和線段
和線段![]() 交點,
交點,
![]() 時,
時,![]() ,且
,且![]()
解得![]() ;
;
綜上所述:![]() 或
或![]() .
.


 課時訓練江蘇人民出版社系列答案
課時訓練江蘇人民出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知點A(3,4),點B為直線x=﹣2上的動點,點C(x,0)且﹣2<x<3,BC⊥AC垂足為點C,連接AB.若AB與y軸正半軸的所夾銳角為α,當tanα的值最大時x的值為( )

A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,一次函數![]() (a,b為常數,且
(a,b為常數,且![]() )與反比例函數
)與反比例函數![]() (m為常數,且
(m為常數,且![]() )的圖象交于點A(﹣2,1)、B(1,n).
)的圖象交于點A(﹣2,1)、B(1,n).

(1)求反比例函數和一次函數的解析式;
(2)連結OA、OB,求△AOB的面積;
(3)直接寫出當![]() 時,自變量x的取值范圍.
時,自變量x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地質量監管部門對轄區內的甲、乙兩家企業生產的某同類產品進行檢查,分別隨機抽取了 50 件產品并對某一項關鍵質量指標做檢測,獲得了它們的質量指標值 s ,并對樣本數據(質量指標值 s )進行了整理、描述和分析.下面給出了部分信息.
a.該質量指標值對應的產品等級如下:
質量指標值 | 20 ≤ s 25 | 25 ≤ s 30 | 30 ≤ s 35 | 35 ≤ s 40 | 40 ≤ s ≤ 45 |
等級 | 次品 | 二等品 | 一等品 | 二等品 | 次品 |
說明:等級是一等品,二等品為質量合格(其中等級是一等品為質量優秀); 等級是次品為質量不合格.
b.甲企業樣本數據的頻數分布統計表如下(不完整):
c.乙企業樣本數據的頻數分布直方圖如下:
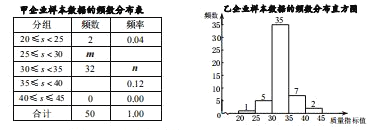
d.兩企業樣本數據的平均數、中位數、眾數、方差如下:
平均數 | 中位數 | 眾數 | 方差 | |
甲企業 | 31.92 | 32.5 | 34 | 11.87 |
乙企業 | 31.92 | 31.5 | 31 | 15.34 |
根據以上信息,回答下列問題:
(1) m 的值為 , n 的值為 ;
(2)若從甲企業生產的產品中任取一件,估計該產品質量合格的概率為 ; 若乙企業生產的某批產品共5 萬件,估計質量優秀的有 萬件;
(3)根據圖表數據,你認為 企業生產的產品質量較好,理由為 .(從某個角度說明推斷的合理性)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列各問題中,兩個變量之間的關系不是反比例函數的是
A. 小明完成100m賽跑時,時間t(s)與跑步的平均速度v(m/s)之間的關系.
B. 菱形的面積為48cm2,它的兩條對角線的長為y(cm)與x(cm)的關系.
C. 一個玻璃容器的體積為30L時,所盛液體的質量m與所盛液體的體積V之間的關系.
D. 壓力為600N時,壓強p與受力面積S之間的關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1的菱形ABCD中,∠ABC=60°,將△ABD沿射線BD的方向平移得到△A'B'D',分別連接A'C,A'D,B'C,則A'C+B'C的最小值為_____.
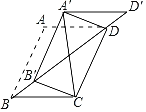
查看答案和解析>>
科目:初中數學 來源: 題型:
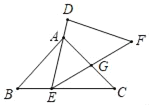
【題目】如圖,在△ABC中,已知,AB=AC=6,BC=10.E是C邊上一動點(E不與點B、C重合),△DEF≌△ABC.其中點A,B的對應點分別是點D、E,且點E在運動時,DE邊始終經過點A,設EF與AC相交于點G,當△AEG為等腰三角形時,則BE的長為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com