
【題目】如圖,∠BAC=90°,AB=AC,D點在AC上,E點在BA的延長線上,BD=CE,BD的延長線交CE于F.證明: 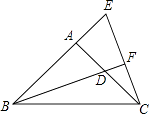
(1)AD=AE
(2)BF⊥CE.
科目:初中數學 來源: 題型:
【題目】如圖,(10分)AB∥DE,試問∠B、∠E、∠BCE有什么關系.

解:∠B+∠E=∠BCE
過點C作CF∥AB,
則![]() ____( )
____( )
又∵AB∥DE,AB∥CF,
∴____________( )
∴∠E=∠____( )
∴∠B+∠E=∠1+∠2
即∠B+∠E=∠BCE.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了鼓勵市民節約用水,某市水費實行分段計費制,每戶每月用水量在規定用量及以下的部分收費標準相同,超出規定用量的部分收費標準相同.例如:若規定用量為10噸,每月用水量不超過10噸按1.5元/噸收費,超出10噸的部分按2元/噸收費,則某戶居民一個月用水8噸,則應繳水費:8×1.5=12(元);某戶居民一個月用水13噸,則應繳水費:10×1.5+(13﹣10)×2=21(元).
表是小明家1至4月份用水量和繳納水費情況,根據表格提供的數據,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(噸) | 6 | 7 | 12 | 15 |
水費(元) | 12 | 14 | 28 | 37 |
(1)該市規定用水量為 噸,規定用量內的收費標準是 元/噸,超過部分的收費標準是 元/噸.
(2)若小明家五月份用水20噸,則應繳水費 元.
(3)若小明家六月份應繳水費46元,則六月份他們家的用水量是多少噸?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知如圖,在數軸上點![]() ,
, ![]() 所對應的數是
所對應的數是![]() ,
, ![]() .
.
對于關于![]() 的代數式
的代數式![]() ,我們規定:當有理數
,我們規定:當有理數![]() 在數軸上所對應的點為
在數軸上所對應的點為![]() 之間(包括點
之間(包括點![]() ,
, ![]() )的任意一點時,代數式
)的任意一點時,代數式![]() 取得所有值的最大值小于等于
取得所有值的最大值小于等于![]() ,最小值大于等于
,最小值大于等于![]() ,則稱代數式
,則稱代數式![]() ,是線段
,是線段![]() 的封閉代數式.
的封閉代數式.
例如,對于關于![]() 的代數式
的代數式![]() ,當
,當![]() 時,代數式
時,代數式![]() 取得最大值是
取得最大值是![]() ;當
;當![]() 時,代數式
時,代數式![]() 取得最小值是
取得最小值是![]() ,所以代數式
,所以代數式![]() 是線段
是線段![]() 的封閉代數式.
的封閉代數式.
問題:(![]() )關于
)關于![]() 代數式
代數式![]() ,當有理數
,當有理數![]() 在數軸上所對應的點為
在數軸上所對應的點為![]() 之間(包括點
之間(包括點![]() ,
, ![]() )的任意一點時,取得的最大值和最小值分別是__________.
)的任意一點時,取得的最大值和最小值分別是__________.
所以代數式![]() __________(填是或不是)線段
__________(填是或不是)線段![]() 的封閉代數式.
的封閉代數式.
(![]() )以下關
)以下關![]() 的代數式:
的代數式:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
是線段![]() 的封閉代數式是__________,并證明(只需要證明是線段
的封閉代數式是__________,并證明(只需要證明是線段![]() 的封閉代數式的式子,不是的不需證明).
的封閉代數式的式子,不是的不需證明).
(![]() )關于
)關于![]() 的代數式
的代數式![]() 是線段
是線段![]() 的封閉代數式,則有理數
的封閉代數式,則有理數![]() 的最大值是__________,最小值是__________.
的最大值是__________,最小值是__________.
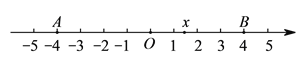
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等邊△ABC中,M為BC邊上的中點,D是射線AM上的一個動點,以CD為一邊且在CD的下方作等邊△CDE,連接BE. 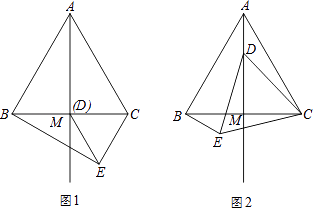
(1)填空:若D與M重合時(如圖1)∠CBE=度;
(2)如圖2,當點D在線段AM上時(點D不與A、M重合),請判斷(1)中結論是否成立?并說明理由;
(3)在(1)的條件下,若AB=6,試求CE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com