
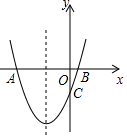
 如圖,拋物線y=x2+2x+k+1與x軸交與A、B兩點,與y軸交與點C(0,-3).
如圖,拋物線y=x2+2x+k+1與x軸交與A、B兩點,與y軸交與點C(0,-3).分析 (1)由拋物線y=x2+2x+k+1與y軸交于點C(0,-3),即可將點C的坐標代入函數解析式,解方程即可求得k的值,由拋物線y=x2+2x+k+1即可求得拋物線的對稱軸為:x=-1;
(2)連接AC交拋物線的對稱軸于點P,則PA+PC的值最小,求得A與C的坐標,設直線AC的解析式為y=kx+b,利用待定系數法即可求得直線AC的解析式,則可求得此時點P的坐標;
(3)①設點M的坐標為:(x,(x+1)2-4),即可得S△AMB=$\frac{1}{2}$×4×|(x+1)2-4|,由二次函數的最值問題,即可求得△AMB的最大面積及此時點M的坐標;
②設點M的坐標為:(x,(x+1)2-4),然后過點M作MD⊥AB于D,由S四邊形ABCM=S△OBC+S△ADM+S梯形OCMD,根據二次函數的最值問題的求解方法,即可求得四邊形AMCB的最大面積及此時點M的坐標.
解答 解:(1)∵拋物線y=x2+2x+k+1與y軸交于點C(0,-3),
∴-3=1+k,
∴k=-4,
∴拋物線的解析式為:y=(x+1)2-4,
∴拋物線的對稱軸為:直線x=-1;
(2)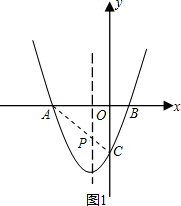 如圖1,連接AC交拋物線的對稱軸于點P,則PA+PC的值最小,
如圖1,連接AC交拋物線的對稱軸于點P,則PA+PC的值最小,
當y=0時,(x+1)2-4=0,
解得:x=-3或x=1,
∵A在B的左側,
∴A(-3,0),B(1,0),
設直線AC的解析式為:y=kx+b,則
$\left\{\begin{array}{l}{-3k+b=0\\;}\\{b=-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=-3}\end{array}\right.$,
∴直線AC的解析式為:y=-x-3,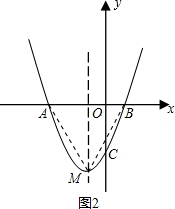
當x=-1時,y=-(-1)-3=-2,
∴點P的坐標為:(-1,-2);
(3)如圖2,點M是拋物線上的一動點,且在第三象限,
∴-3<x<0;
①設點M的坐標為:(x,(x+1)2-4),
∵AB=1-(-3)=4,
∴S△AMB=$\frac{1}{2}$×4×|(x+1)2-4|=2|(x+1)2-4|,
∵點M在第三象限,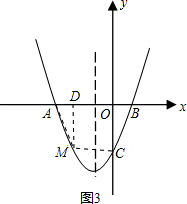
∴S△AMB=8-2(x+1)2,
∴當x=-1時,即點M的坐標為(-1,-4)時,△AMB的面積最大,最大值為8;
②設點M的坐標為:(x,(x+1)2-4),
如圖3,過點M作MD⊥AB于D,則
S四邊形ABCM=S△OBC+S△ADM+S梯形OCMD
=$\frac{1}{2}$×3×1+$\frac{1}{2}$×(3+x)×[4-(x+1)2]+$\frac{1}{2}$×(-x)×[3+4-(x+1)2]
=-$\frac{3}{2}$(x2+3x-4)
=-$\frac{3}{2}$(x+$\frac{3}{2}$)2+$\frac{75}{8}$,
∴當x=-$\frac{3}{2}$時,y=(-$\frac{3}{2}$+1)2-4=-$\frac{15}{4}$,
即當點M的坐標為(-$\frac{3}{2}$,-$\frac{15}{4}$)時,四邊形AMCB的面積最大,最大值為$\frac{75}{8}$.
點評 此題屬于二次函數綜合題,主要考查了待定系數法求函數的解析式,二次函數的最值,三角形與四邊形的面積問題以及線段和最短問題等知識的綜合應用.解題的關鍵是運用方程思想與數形結合思想進行求解.


科目:初中數學 來源: 題型:選擇題
| A. | 0既不是正數也不是負數 | B. | 絕對值最小的數是0 | ||
| C. | 一個有理數不是整數就是分數 | D. | 數a的倒數是$\frac{1}{a}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
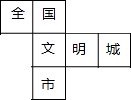 在市委、市政府的領導下,全市人民齊心協力,力爭于2017年將我市創建為“全國文明城市”,為此小宇特制了正方體模具,其展開圖如圖所示,原正方體中與“文”字所在的面正對面上標的字是( )
在市委、市政府的領導下,全市人民齊心協力,力爭于2017年將我市創建為“全國文明城市”,為此小宇特制了正方體模具,其展開圖如圖所示,原正方體中與“文”字所在的面正對面上標的字是( )| A. | 全 | B. | 國 | C. | 明 | D. | 城 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 8 | B. | 7 | C. | 8或7 | D. | 9或8 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com